2015-09-06
1361
Определим пространственный масштаб разделения зарядов. Представим, что в некотором объеме плазмы нейтральность нарушена. Для простоты будем считать, что это нарушение происходит в результате смещения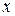 
плоского слоя электронов. При этом образуются слои отрицательного и положительного объемных зарядов. Электрическое поле между слоями эквивалентно полю плоского конденсатора. Напряженность поля 
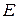определяется поверхностной плотностью заряда 
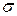на «обкладках»:
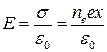, [ед.СИ]
где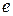 
-заряд; 
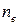-плотность электронов; 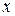-смещение слоя. Вычислим работу по разделению зарядов на расстояние d, которая совершается силами возникающего на длине x электрического поля 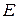. С учетом того, что сила, действующая на электрон равна eE, работа этой силы равна 
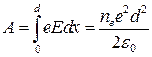. Эта работа не может превышать кинетическую энергию теплового движения частиц плазмы, которая для случая одномерного движения равна 
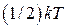, где k – постоянная Больцмана, T – температура, т.е. 
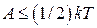. Из этого условия следует оценка максимального пространственного масштаба разделения заряда
|
|
|
.
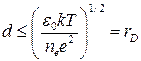Более строгие расчеты дают
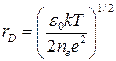. (6)
Эта величина называется радиусом Дебая по имени ученого, который ввел ее впервые. Радиус Дебая является важнейшей характеристикой плазмы. В частности, электрическое поле, создаваемое каждой отдельной заряженной частицей в плазме, экранируется частицами противоположного знака и фактически исчезает на расстоянии порядка радиуса Дебая от самой частицы. С другой стороны, величина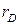 
определяет глубину проникновения внешнего электрического поля в плазму.
