2015-09-06
490
Основная идея этого кориляционного метода – по ЛС передаётся сигнал, являющийся суммой закодированных (при помощи системы сигналов-носителей) сигналов Uk(t). На выходе для соотв. абонента сигнал U(t) умножается на соотв. сигнал-носитель gk из системы и интегрируется.
Сигнал, поступающий в линию связи U(t)=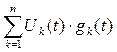 
.
Если gk(t) линейно независимы, они могут быть разделены линейными фильтрами. Такие многоканальные системы передачи носят название линейных. В этом случае используют системы ортонормированных сигналов.
Сигнал, принятый из линии связи, умножается на gk(t) и затем интегрируется:
U(t)*gk(t) = gk(t)* [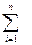 
Ui(t)*gi(t)].
Интегрируется:
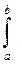gk(t)* [ 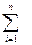Ui(t)*gi(t)]* dt, где a, b – интервал времени, на котором система функций gk(t) ортонормированна.
Внесем под знак суммы gk(t)
= 
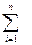
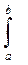Ui(t)*gi(t)*gk(t)*dt. *
Интегрирование по частям:
òp*dv=pv - òv*dp.
Для этого интеграл 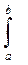Ui(t)*gi(t)*gk(t)*dt представим в виде
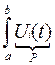*d [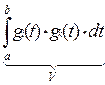 
] = Ui(t)* 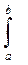gi(t)*gk(t)*dt - 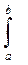( 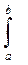gi(t)*gk(t)*dt)*d [Ui(t)].
Для i≠k по свойству ортогональности функций 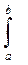gi(t)*gk(t)*dt=0 -> Ui(t)*0 - 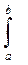(0)*d[Ui(t)] =0.
Для i=k по свойству нормированности функций 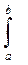g2k(t)*dt=1, Uk(t)*1 - 
=
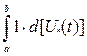Uk(t)*1 - Uk(t)│ 
= Uk(t) - [Uk(b)-Uk(a)].
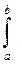gk(t)* [ 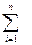Ui(t)*gi(t)]* dt = Uk(t) - [Uk(b)-Uk(a)].
В полученном результате Uk(a) – значение сигнала k-того источника сигнала в начальный момент времени, Uk(b) – значение сигнала k-того источника сигнала в конце передачи.
На выходе интегратора - передаваемый сигнал, смещенный по оси ординат. Смещение устраняется посредством пропускания через конденсатор.
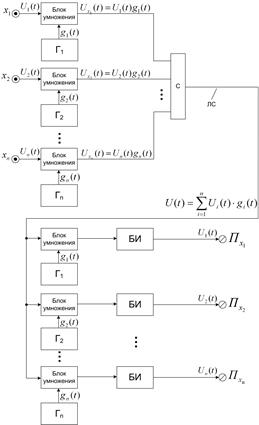
Структурная схема многоканальной системы с кодовым разделением:
Г1 ÷Гn – генераторы сигналов ортонормированный системы сигналов g1 ÷ gn; С – сумматор; БИ – блоки интегрирования;
”+”
Меньшее влияние перекрестных помех.
Комбинированные методы разделения
Используются для увеличения числа каналов и уменьшения их взаимного влияния.
#, разделение по форме + частотное/временное = количество каналов в 2 раза больше.
Применяются комбинации частотного с временным, кодового с частотным и другие.
