Вопрос №21. Доказать общий случай приведения произвольной пространственной системы сил к динамическому винту

Совокупность силы, равной главному вектору, и пары сил с моментом, равным главному моменту, коллинеарным главному векто­ру, называется динамическим винтом или динамой.

Пусть в произвольном центре О система сил приведена к главному вектору R и главному моменту М₀.

Разложим главный момент М₀ на две составляющие (рис. 1.34), направленные по главному вектору и перпендикулярно к нему:

М₀ = М* + М₁. (I)

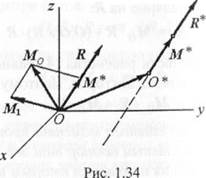Величина вектора М*, равная проекции главного момента на направление главного вектора, не зависит от выбора центра приведения, т.е.

М* = const,

причем численно

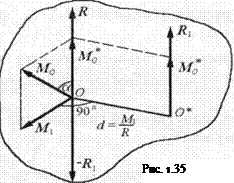С изменением центра приведения будет изменяться только пендикулярная составляющая М1. Мы всегда можем найти такой центр приведения О*, чтобы переменная составляющая М1 обратилась в нуль.Тогда главный момент и главный вектор будут коллинеарны, а вектор М*0 будет иметь минимальную величину, определяемую формулой (2). Составляющая М1 представляет собой момент пары сил, плоскость которой перпендикулярна М1 (рис. 1.35) Выберем силы R1 и –R1, состовляющие эту пару,равны по модулю главному вектору R и приложим силу –R1к центру приведения О. Система сил R и –R₁ приложенная к точке О, как эквивалента нулю может быть отброшена. Так как момент М* - вектор свободный, то его можно перенести из точки О в О*. Таким образом, заданная система сил приведена в центре О* к одной силе R1 = R и к паре сил с моментом М*,то есть мы получили динамический винт.

Точка О не единственная, в которой система приводится к динаме. В самом деле, силу R можно переносить вдоль линии ее действия, момент же пары сил есть вектор свободный. Следовательно, система сил может быть приведена к динаме во всех точках прямой, проходя­щей через центр приведения О* и являющейся линией действия главно­го вектора R1 = R.

Геометрическое место центров приведения, относительно которых главный момент коллинеарен главному вектору, называется центральной осью данной системы сил.

Так как на центральной оси главный момент имеет минималь­ное значение, эта ось называется осью наименьших главных моментов.

Найдем теперь уравнение центральной оси. Пусть О* точка цен­тральной оси. Тогда

М*= M₀+О*OхR= М_о-ОО*хR. (3)

Условие коллинеарности главного вектора и главного момента для точ­ки О* записываем следующим образом:

M* = pR. (4)

Здесь р - постоянная величина, имеющая размерность длины, называемая параметром винта.

Т.к. величина минимального момента М* определяется формулой (2), то

Очевидно, что знак параметра определяется знаком второго инварианта. При р > 0, R и М* направлены в одну сторону.

Подставляя в формулу (4) значение минимального момента М* из (3), получим

M₀-ОO*xR =pR. (6)

Таким образом нами получено уравнение центральной оси в векторной форме, причем текущей координатой является вектор ОО*. Если координаты векторов М₀, R и ОО* обозначить

Мо(М_X,М_у, М_z), R(R_X, R_y R_z:), OO*(х, у, z), то в проекциях на оси координат уравнение центральной оси примет вид

М_х – (yR_z - zR_y) М_у - (zR_x - xR_z) M_z - (xR_y - yR_x)

Rx Ry Rz

Итак, всякая система сил, действующая на твердое тело, для которой второй инвариант не равен нулю, приводится к динаме.