Таким образом, систематические погрешности можно устранить, промахи следует отбросить, случайные погрешности оцениваются в теории погрешностей

1 2 3 4 5 6 7

МеханикА

Методические указания

к лабораторным работам по физике

для студентов 1-го курса технических специальностей

всех форм обучения

Ростов-на-Дону

Вводное занятие

Тема: Элементарная оценка погрешностей физических измерений

Физические измерения

1. Прямыми называются измерения, в которых значение измеряемой величины получается непосредственно в процессе измерения. Пример: измерение длины ¾ линейкой, времени ¾ секундомером, силы тока ¾ амперметром.

2. Косвенными называют измерения, в которых значение определяемой величины находят вычислением по формуле, в которую входят данные измерений других физических величин. Косвенными измерениями является, например, определение плотности тела по результатам измерений массы и размеров тела.

3. Классификация погрешностей (ошибок измерений).

По происхождению погрешности можно разделить на три типа: систематические, случайные и промахи.

Cистематические погрешности связаны с несовершенством средств и методов измерений.

При многократном измерении одной и той же величины они сохраняются постоянными или меняются по определенному закону. Поэтому их можно полностью исключить введением поправок на показания приборов, их тщательной отладкой и т. д.

Промахами называются погрешности, которые могут возникнуть в результате ошибочно отсчитанных или записанных показаний приборов, неисправностей или неверного подключения прибора и т. д. Измерения, содержащие промахи, следует отбрасывать.

Случайные погрешности не подчиняются какому-либо закону и при многократном измерении одной и той же физической величины случайным образом меняют свое значение.

Таким образом, систематические погрешности можно устранить, промахи следует отбросить, случайные погрешности оцениваются в теории погрешностей.

4. Вычисление погрешностей прямых измерений.

Абсолютная погрешность измерения D х показывает на сколько полученный нами результат отличается от истинного. Для этого измерения проводят несколько раз. В качестве истинного значения измеряемой величины принимается среднее арифметическое значение результатов измерений:

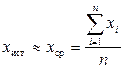где х_i (i = 1, 2, 3, ¼n) ¾ результат i -го измерения; n ¾ число измерений.

Далее необходимо найти абсолютную погрешность каждого из проведенных измерений:

D х_i = ê х_i - х _срê.

В качестве абсолютной погрешности D х можно принять величину:

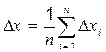Результат принято записывать в виде:

х = х _ср ± D х.

Относительная погрешность d х равна отношению абсолютной погрешности измерения к среднему значению измеряемой величины.

d х = (D х / х _ср).

5. Вычисление погрешностей косвенных измерений.

При косвенных измерениях искомая величина является функцией других измеряемых величин, поэтому сначала, по заданной в методическом указании формуле, необходимо рассчитать относительную погрешность измерения d х, а затем определить абсолютную погрешность измерения

D х = х _эк d х.

Ответ необходимо представить в виде:

х = (х _эк± D х), d х = ¼.