Цель работы
1.1. Изучение свободных незатухающих, свободных затухающих и вынужденных колебаний пружинного маятника.
1.2. Определение логарифмического декремента затухания и коэффициента сопротивления воздуха.
1.3. Определение резонансной частоты.
Теоретическая часть
Колебательным движением (колебанием) называют движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Колебание называют периодическим, если значение колеблющейся со временем величины (например, координаты тела, его скорости, ускорения) в точности повторяется через равные промежутки времени. Наименьший промежуток времени, через который это происходит, называют периодом колебания.
Свободными (собственными) называют такие колебания, которые происходят в системе, предоставленной самой себе после того как она была выведена из положения равновесия. Свободные незатухающие колебания – колебания с неизменной амплитудой (амплитудой колебания называют наибольшее отклонение колеблющейся величины от равновесного значения). Свободными затухающими колебаниями называют такие колебания, амплитуда которых с течением времени уменьшается.
Колебания, при которых колеблющаяся величина изменяется со времен по закону косинуса или синуса, называют гармоническими, т.е. если величина х совершает гармоническое колебание, то она изменяется со временем по закону
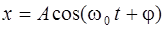 , (2.1)
, (2.1)
где 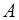 – амплитуда колебания;
– амплитуда колебания; 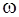 – круговая или циклическая частота;
– круговая или циклическая частота;
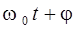 – фаза колебания, определяющая значение х в данный момент времени t;
– фаза колебания, определяющая значение х в данный момент времени t; 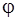 0 – фаза колебания в начальный момент времени t = 0, называемая начальной фазой.
0 – фаза колебания в начальный момент времени t = 0, называемая начальной фазой.
Если х представляет собой координату тела, то скорость 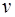 и ускорение
и ускорение 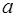 при гармоническом колебании изменяются со временем по законам
при гармоническом колебании изменяются со временем по законам
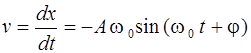 , (2.2)
, (2.2)
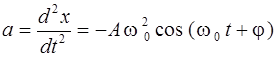 . (2.3)
. (2.3)
Из уравнений (2.3) и (2.1) имеем
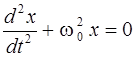 . (2.4)
. (2.4)
Это уравнение, решением которого является гармоническая функция (2.1), называют дифференциальным уравнением свободных незатухающих гармонический колебаний.
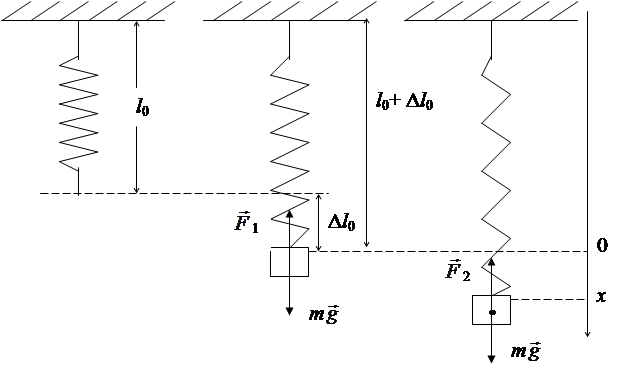
Примером гармонических колебаний служат колебания пружинного маятника, представляющего собой груз, прикрепленный к упругой пружине. Если 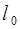 – первоначальная длина пружины без груза, то при подвешивании груза массы m пружина растянется на величину Δ
– первоначальная длина пружины без груза, то при подвешивании груза массы m пружина растянется на величину Δ 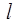 , называемую статическим удлинением пружины рис. 2.1.
, называемую статическим удлинением пружины рис. 2.1.
 |
•
Рис. 2.1
Когда маятник находится в положении равновесия, сила тяжести, действующая на груз, уравновешивается силой упругости пружины. Если удлинение пружины невелико, то выполняется закон Гука, согласно которому
F 1 = k Δ l
и
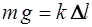 , (2.5)
, (2.5)
где 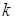 – коэффициент упругости.
– коэффициент упругости.
При смещении груза относительно положения равновесия в положение, где его координата равна 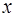 , удлинение пружины будет равно Δ
, удлинение пружины будет равно Δ 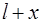 . Для этого положения по второму закону Ньютона имеем
. Для этого положения по второму закону Ньютона имеем
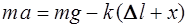 .
.
Откуда, учитывая (2.5) и то, что 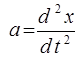 , получаем дифференциальное уравнение свободных незатухающих колебаний
, получаем дифференциальное уравнение свободных незатухающих колебаний
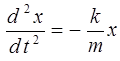 , (2.6)
, (2.6)
совершаемых с частотой
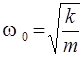 .
.
Таким образом, колебания, совершаемые телом под действием упругой силы или любой другой, не являющейся силой упругости, но также пропорциональной смещению (F ~ x), будут гармоническими. Такие силы называют квазиупругими.
В реальной механической колебательной системе первоначально сообщенная ей энергия при последующих колебаниях уменьшается вследствие работы против сил сопротивления среды. Со временем максимальное значение отклонения от положения равновесия, скорости и ускорения тела уменьшаются. Такое колебательное движение не является строго периодическим. Поэтому при описании затухающих колебаний понятия амплитуды, периода, частоты можно использовать лишь условно.
Закон убывания амплитуды зависит от характера сил сопротивления среды. При малых скоростях сила сопротивления среды прямо пропорциональна скорости
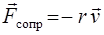 ,
,
где r – коэффициент сопротивления среды.
Уравнение динамики тела при его движении под действием сил упругости и сопротивления среды будет иметь вид
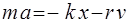 . (2.7)
. (2.7)
Откуда
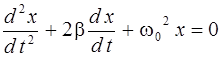 , (2.8)
, (2.8)
где 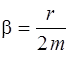 называют коэффициентом затухания.
называют коэффициентом затухания.
Уравнение (2.8) называют дифференциальным уравнением свободных затухающих колебаний. Решением уравнения (2.8) является функция х (t) вида
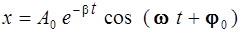 , (2.9)
, (2.9)
где А 0 и j 0 – начальные амплитуда и фаза колебаний, определяемые начальными условиями.
Судя по уравнению (2.9), можно рассматривать изменение х со временем как гармоническое колебание с изменяющейся со временем амплитудой
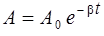 . (2.10)
. (2.10)
Циклическая частота затухающих колебаний оказывается равной
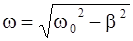 .
.
Величину 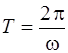 называют периодом затухающих колебаний.
называют периодом затухающих колебаний.
Основными величинами, характеризующими затухающие колебания в системе, служат: логарифмический декремент затухания, время релаксации и добротность.
Логарифмическим декрементом затухания l называют натуральный логарифм отношения двух последовательных амплитуд, отстоящих на время, равное периоду:
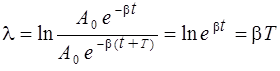 .
.
Время t, за которое амплитуда затухающих колебаний уменьшается в е раз, называют временем релаксации. Можно показать, что
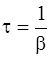 .
.
Величину
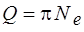 , (2.11)
, (2.11)
где Ne – число колебаний за время релаксации, называют добротностью колебательной системы.
Добротность равна умноженному на 2p отношению запасенной в системе энергии Е к энергии D Е, теряемой за период
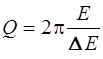 .
.
При малых значениях b 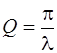 .
.
Вынужденными колебаниями называют колебания, которые происходят под действием внешней, периодически изменяющейся со времен силы (F = f (t)). Если вынуждающая внешняя сила изменяется по гармоническому закону F = F 0 cos w t, то уравнение динамики тела в любой момент времени можно представить в виде
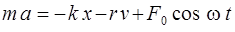 , (2.12)
, (2.12)
или
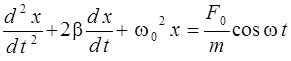 . (2.13)
. (2.13)
Это уравнение называют дифференциальным уравнением вынужденных колебаний. Его решение имеет вид
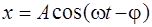 , (2.14)
, (2.14)
где значения А и j определяются уравнениями
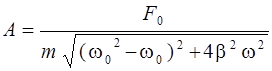 ,
, 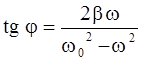 (2.15)
(2.15)
Таким образом, вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и зависит от ее частоты.
При вынужденных колебаниях может возникнуть резонанс. Резонансом называют явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы w к частоте собственных колебаний системы w 0.
Резонансная частота для х оказывается равной
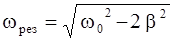 , (2.16)
, (2.16)
а амплитуда при резонансе
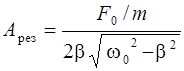 . (2.17)
. (2.17)
Согласно (2.16), резонансная частота в отсутствие сопротивления среды (при b = 0) совпадает с собственной частотой колебательной системы.
 2015-10-16
2015-10-16 384
384







