Моментом инерции материальной точки относительно оси называют величину

ЛАБОРАТОРНАЯ РАБОТА № 4

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы

Исследование крутильных колебаний и измерение момента инерции тела сложной формы.

Теоретическая часть

Момент инерции. Теорема Штейнера

Моментом инерции материальной точки относительно оси называют величину

,

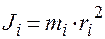где m_i – масса материальной точки, r_i – расстояние от материальной точки до оси.

Моментом инерции тела относительно оси называют сумму моментов инерции материальных точек, составляющих его

.

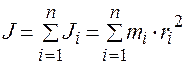Представляя тело состоящим из малых частей объемом dV и массы dm, его момент инерции можно рассчитать интегрированием

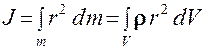, (2.1)

где ρ – плотность.

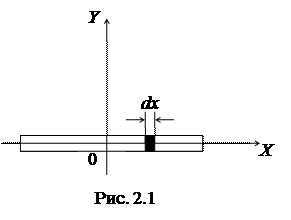
Рассчитаем, например, момент инерции тонкого однородного стержня массы m и длины l относительно оси перпендикулярной стержню и проходящей через его середину (рис. 2.1).

			Выделим элемент стержня массы dm, длины dх, отстоящий на расстоянии х от центра стержня. Момент инерции этого элемента относительно оси 0 y d J = х 2 dm = х 2 m / l dх, а момент инерции всего стержня относительно этой оси будет рррр

равен 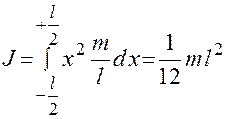. (2.2)

Из (2.1) следует, что момент инерции однородного стержня не зависит от его ширины, поэтому формула (2.2) применима для расчета момента инерции тонкой однородной пластины прямоугольной формы.

Если известен момент инерции тела относительно оси, проходящей через центр масс, то момент инерции тела относительно любой параллельной оси можно определить, воспользовавшись теоремой Штейнера, согласно которой момент инерции J тела относительно произвольной оси равен сумме момента инерции J_с тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями

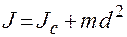. (2.3)

Представим параллелепипед в виде совокупностей сплошных пластин толщиной dу, длиной b, шириной с, массой dm, отстоящей на расстояние у от оси 0Z рис.2.2. Момент инерции одной пластины относительно оси 0Z определим, используя теорему Штейнера

Используя уравнение (2.2), теорему Штейнера и уравнение (2.1) рассчитаем момент инерции параллелепипеда относительно оси симметрии.

	y

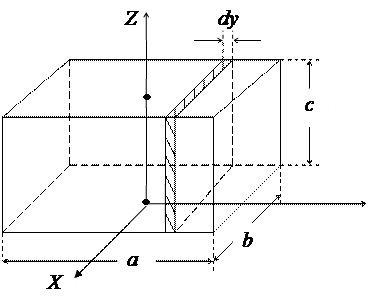
Рис. 2.2

.

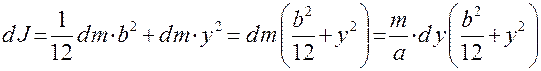Момент инерции параллелепипеда относительно оси 0Z

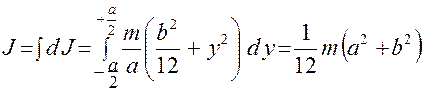, (2.4)

где а и b – длины сторон параллелепипеда, расположенные в горизонтальной плоскости, m – масса параллелепипеда.

Момента инерции тела относительно оси является мерой инертности тела при вращательном движении и зависит не только от массы тела, но и от распределения ее в пространстве относительно оси. Тело обладает определенным моментом инерции относительно любой оси независимо от того вращается оно или покоится.