2017-12-14
1386
Центробежный момент инерции относительно двух осей координат называется сумма произведений массы каждой из точек тела на координаты вдоль соответствующих осей.
Если тело имеет ось симметрии, то центробежный момент инерции тела равен нулю и оси у, х являются главными
18. Теорема Гюйгенса-Штейнера о вычислении моментов относительно параллельных осей .
Момент инерции твёрдого тела относительно оси не проходящей через центр масс равен сумме моментов инерции относительно центральной оси проходящей через центр масс и параллельной заданной и произведение массы тела на квадрат расстояния между осями.
где
JC — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.
Вычисление моментов инерции однородных тел: тонкая пластина, тонкий стержень, кольцо, цилиндр, конус.
Тонкий стержень: 
Тонкий цилиндр: 
Тонкая пластина: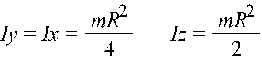 
Конус: 
Тонкое кольцо: 
Шар: 
Вычисление моментов инерции относительно произвольных осей.
Позволяет найти момент инерции относительно любой оси проходящей через оси координат и составляющие угля
с этими осями, через величины осевых и центробежных моментов инерции этих осей.
