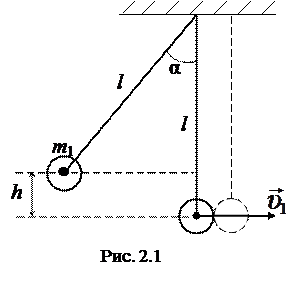
Рассмотрим два шара, подвешенных рядом так, что их центры находятся на одном уровне. Отведем один из шаров на некоторый угол α и отпустим без начальной скорости. Отклоненный шар будет двигаться вниз, разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую. По закону сохранения механической энергии (рис. 2.1)
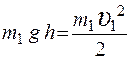 , (2.1)
, (2.1)
где m 1 – масса шара, g – ускорение свободного падения, h – высота шара в отведенном положении относительно нижней точки траектории, υ 1 – скорость первого шара в нижней точке перед соударением со вторым.
Из рисунка видно, что
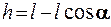 , (2.2)
, (2.2)
где l – расстояние от точки подвеса до центра тяжести шара, α – угол начального отклонения нити.
Подставляя (2.2) в (2.1) и преобразуя уравнение, найдем выражение для скорости через угол начального отклонения
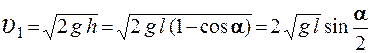 . (2.3)
. (2.3)
Если подобрать массы шаров так, чтобы после удара они разлетались в разные стороны на углы α1 и α2 соответственно, то скорости 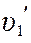 и
и 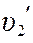 (рис. 2.2) шаров после удара
(рис. 2.2) шаров после удара
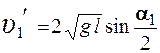 , (2.4)
, (2.4)
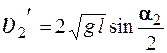 .
.
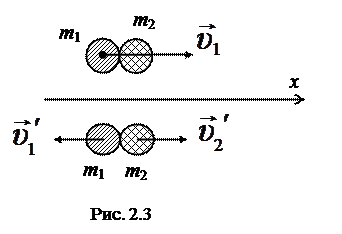
Если удар происходит достаточно быстро так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси х не возникает внешних сил и выполняется закон
сохранения импульса в проекции на эту ось
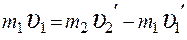 . (2.5)
. (2.5)
Коэффициент восстановления скорости КС определяется как отношение относительной скорости шаров после удара к относительной скорости шаров до удара
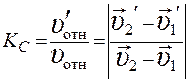 . (2.6)
. (2.6)
Для случая, показанного на рис.2.1 и рис.2.2 формулу (2.6) с учетом (2.3) и (2.4) преобразуем к виду
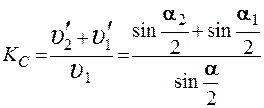 . (2.7)
. (2.7)
Для абсолютно упругого удара КС = 1. В случае столкновения реальных шаров столкновение не является абсолютно упругим и КС < 1.
Кроме коэффициента восстановления скорости соударения тел характеризуют коэффициентом восстановления энергии КЭ, равным отношению кинетической энергии тел после удара к их кинетической энергии до удара
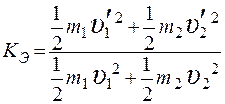 . (2.8)
. (2.8)
Учитывая, что скорость второго шара до удара υ 2 = 0 и подставляя для скоростей выражения (2.3) и (2.4), находим рабочую формулу для коэффициента восстановления энергии
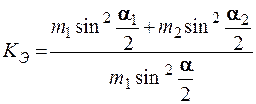 . (2.9)
. (2.9)
Согласно второму закону Ньютона, сила, действующая на тело, равна скорости изменения импульса этого тела
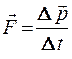 . (2.10)
. (2.10)
Если известна длительность удара τ, то используя (2.10) по изменению импульса одного из шаров (например, покоящегося до удара) можно определить среднюю силу взаимодействия между шарами
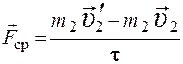
или
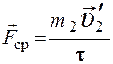 . (2.11)
. (2.11)
 2015-10-16
2015-10-16 1654
1654
