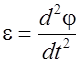Лабораторная работа № 9
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
С ПОМОЩЬЮ ФИЗИЧЕСКОГО И МАТЕМАТИЧЕСКОГО
МАЯТНИКОВ
ЦЕЛЬ РАБОТЫ
1.Определение ускорения свободного падения с помощью математического маятника.
2.Определение ускорения свободного падения с помощью оборотного маятника.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Математическим маятником называют систему, состоящую из материальной точки, подвешенной на нерастяжимой невесомой нити, способную совершать колебания в поле силы тяжести.
Физическим маятником называется твердое тело, способное совершать колебания вокруг некоторой оси, не проходящей через его центр инерции. В положении равновесия центр инерции маятника
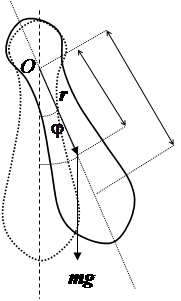
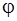 возникает вращательный момент силы тяжести возникает вращательный момент силы тяжести 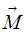 относительно горизонтальной оси, проходящей через точку О, равный: относительно горизонтальной оси, проходящей через точку О, равный:
где | |||||||||
Модуль момента силы тяжести равен:
М=l mg 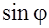 ,
где l – расстояние от точки подвеса до точки приложения силы тяжести, т.е. до центра инерции тела. ,
где l – расстояние от точки подвеса до точки приложения силы тяжести, т.е. до центра инерции тела.
| |||||||||
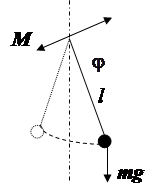
где I __ момент инерции тела относительно оси вращения,
Угловое ускорение есть:
|
Уравнение (1) в проекции на ось Z можно расписать в виде:
I 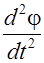 =-mgl sin
=-mgl sin 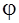 (2)
(2)
Знак минус означает, что направление вектора момента силы тяжести противоположно направлению вектора углового ускорения (рис. 2).
Уравнение (2) приведем к виду:
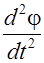 +
+ 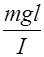 sin
sin 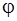 =0(3)
=0(3)
Введем обозначение

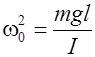
При малых углах отклонения sin 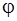
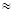
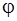 . (Маятник совершает гармонические колебания, если угол отклонения не превышает примерно 8о).Придем к следующему дифференциальному уравнению:
. (Маятник совершает гармонические колебания, если угол отклонения не превышает примерно 8о).Придем к следующему дифференциальному уравнению:
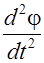 +
+ 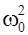
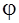 =0
=0
Решение которого имеет вид:
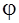 =а cos(
=а cos(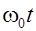 +
+ 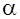 ).
).
Величина а, равная максимальному углу отклонения маятника от положения равновесия, называется амплитудой гармонических колебаний. Величина 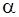 __ начальная фаза,
__ начальная фаза, 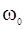 __ циклическая частота.
__ циклическая частота.
Период колебания физического маятника равен:
Т = 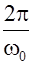 =2
=2 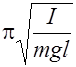
Для математического маятника момент инерции которого равен:
I=ml 2,
выражение для периода колебаний математического маятника будет следующим:
Т =2 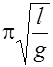 (4)
(4)
Из сопоставления последних двух формул получается, что математический маятник с длиной
l пр = 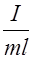
будет иметь такой же период колебаний, как и данный физический маятник. Эту величину называют приведенной длиной физического маятника.
Точка на прямой, соединяющая точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (точка О / на рис. 1)). При переносе точки подвеса в центр качания период колебания маятника будет прежним. Точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания, и период колебаний физического маятника не изменится.
На этом свойстве взаимности основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Он представляет собой маятник (рис 3.), у которого имеются две параллельные друг другу закрепленные вблизи его концов опорные призмы О 1и О 2, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем грузы в виде дисков. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков.
 Рассмотрим произвольный случай, когда упорные призмы находятся в произвольном положении по обеим сторонам от центра тяжести.
Рассмотрим произвольный случай, когда упорные призмы находятся в произвольном положении по обеим сторонам от центра тяжести.
 |
|
Как видно из рис. 3, периоды колебаний маятника по отношению к каждой оси качания будут соответственно равны:
Т 1=2 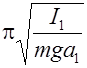 Т 2=2
Т 2=2 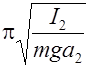 , (5)
, (5)
где I 1, I 2– моменты инерции оборотного маятника относительно осей качания О 1и О 2,
а 1 и а 2– расстояние от центра тяжести маятника до соответствующих осей.
По теореме Штейнера момент инерции I тела относительно произвольной оси равен моменту инерции I 0относительно оси, параллельной данной и проходящей через центр инерции тела, плюс произведение массы тела на квадрат расстояния от оси качания до центра инерции. Используя эту теорему, получим:
I 1= I 0+ m 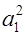 и I 2= I 0 + m
и I 2= I 0 + m 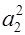 . (6)
. (6)
Тогда с учетом (6):
Т 1=2 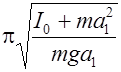 и Т 2=2
и Т 2=2 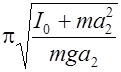 . (7)
. (7)
Если Т 1= Т 2= Т, то приравнивая подкоренные выражения формул (7), получим:
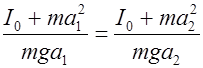 ,
,
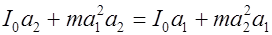 ,
,
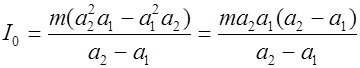
I 0= m а 1 а 2 (8)
Подставляя I 0в формулу (7) для Т 1 получаем
Т =2 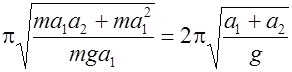 =
= 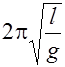 (9)
(9)
В этом случае если О 1–точка подвеса, то О 2 __ центр качания и наоборот, а l есть приведенная длина данного физического маятника.
Ускорение силы тяжести можно найти, зная период колебаний маятника и приведенную длину, т.к. из (9) следует:
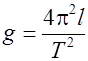 (10)
(10)
Если Т 1 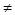 Т 2, то из формул (7) для Т 1и Т 2, получается
Т 2, то из формул (7) для Т 1и Т 2, получается
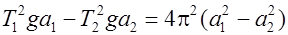 .
.
Отсюда
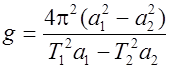 . (11)
. (11)
 2015-10-16
2015-10-16 381
381

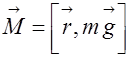
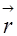 __ радиус вектор, проведенный из точки О до точки приложения силы тяжести, т.е. до центра инерции тела (точка С).
__ радиус вектор, проведенный из точки О до точки приложения силы тяжести, т.е. до центра инерции тела (точка С).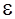
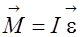 (1)
(1)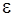 __ угловое ускорение.
__ угловое ускорение.