Рассмотрим простой маятник – тяжелый шарик, подвешенный на длинной нити. Если размеры шарика много меньше длины нити 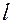 , то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Можно пренебречь и массой нити по сравнению с массой шарика
, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Можно пренебречь и массой нити по сравнению с массой шарика 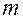 . Таким образом, вместо реального маятника - шарика определенного размера на нити, которая, конечно, немного деформируется при движении и имеет массу, мы вправе рассматривать простую модель - материальную точку, подвешенную на нерастяжимой невесомой нити, называемую математическим маятником.
. Таким образом, вместо реального маятника - шарика определенного размера на нити, которая, конечно, немного деформируется при движении и имеет массу, мы вправе рассматривать простую модель - материальную точку, подвешенную на нерастяжимой невесомой нити, называемую математическим маятником.
Выведем маятник из положения равновесия и отпустим без толчка. Возникнут колебания, проходящие в некоторой вертикальной плоскости. Траекторией движения шарика будет дуга окружности радиусом 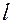 . На шарик при движении будут действовать две силы: сила тяжести
. На шарик при движении будут действовать две силы: сила тяжести 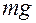 , направленная вертикально вниз и сила упругости нити
, направленная вертикально вниз и сила упругости нити 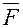 , направленная вдоль нити (рис.2). Конечно, при движении маятника на него еще действует сила сопротивления воздуха, но мы будем считать её пренебрежимо малой.
, направленная вдоль нити (рис.2). Конечно, при движении маятника на него еще действует сила сопротивления воздуха, но мы будем считать её пренебрежимо малой.
Рассмотрим маятник в произвольный момент времени 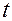 в процессе колебаний.
в процессе колебаний.
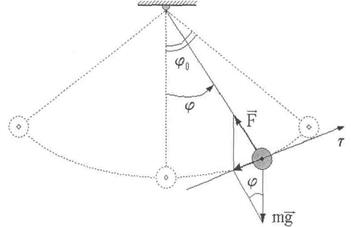
Рис.2
Пусть 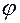 - угол отклонения от вертикали в этот момент. Запишем уравнение второго закона Ньютона в проекции на касательную ось
- угол отклонения от вертикали в этот момент. Запишем уравнение второго закона Ньютона в проекции на касательную ось 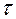 , показанную на рис.2
, показанную на рис.2
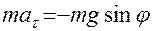 .
.
Принимая во внимание связь линейного 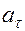 и углового
и углового 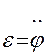 ускорений
ускорений
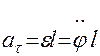
приходим к уравнению
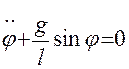 , (8)
, (8)
в котором неизвестная функция 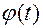 стоит под знаком производной. Такие уравнения в математике называют дифференциальными. Они часто встречаются при решении различных физических задач.
стоит под знаком производной. Такие уравнения в математике называют дифференциальными. Они часто встречаются при решении различных физических задач.
Решение уравнения (8) при произвольном начальном отклонении 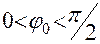 может быть либо найдено только численными методами с применением компьютера, либо записано с помощью специальных функций.
может быть либо найдено только численными методами с применением компьютера, либо записано с помощью специальных функций.
Ограничимся случаем малых колебаний, когда 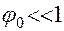 .
.
Как известно из математики, для малых углов 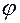
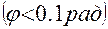 можно воспользоваться соотношением
можно воспользоваться соотношением
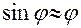 (в радианах). (9)
(в радианах). (9)
Заметим, что соотношение (9) может быть использовано и при углах порядка 30 °
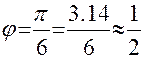 ;
; 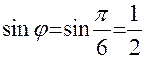 .
.
С учетом соотношения (9) уравнение (8) примет вид
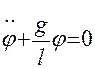 . (10)
. (10)
Уравнения, подобные этому, носят названия уравнений гармонического осциллятора. Непосредственной подстановкой можно убедиться, что решение уравнения (9) имеет вид
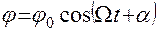 ,
,
где 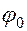 - угловая амплитуда колебаний,
- угловая амплитуда колебаний, 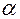 - начальная фаза (в случае, описанном выше
- начальная фаза (в случае, описанном выше 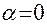 ),
), 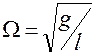 - циклическая частота собственныхколебаний.
- циклическая частота собственныхколебаний.
Для периода колебаний математического маятника имеем
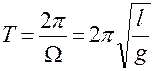 . (11)
. (11)
Из полученного нами соотношения (11) вытекает, что период колебаний 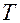 при малых колебаниях
при малых колебаниях 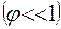 не зависит от амплитуды
не зависит от амплитуды 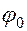 . Это свойство маятника получило название изохронности колебаний.
. Это свойство маятника получило название изохронности колебаний.
В ходе эксперимента Вам предстоит определить диапазон изохронности колебаний и экспериментально проверить зависимость периода малых колебаний 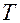 от длины маятника
от длины маятника 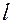 , описываемую теоретически полученным соотношением (11). Соотношение (11) можно преобразовать:
, описываемую теоретически полученным соотношением (11). Соотношение (11) можно преобразовать:
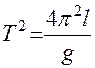 . (12)
. (12)
Для экспериментальной проверки соотношения (12) Вам предстоит измерить периоды малых колебаний маятника при различных значениях длины нити и по результатам измерений построить график зависимости 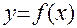 , где
, где 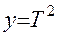 , а
, а 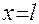 .
.
Если в пределах точности измерений экспериментальные точки ложатся на прямую, то это может являться экспериментальным подтверждением зависимости (11).
Соотношение (12) может быть использовано для определения ускорения свободного падения. Для этого следует измерить период колебаний маятника 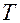 для выбранного значения длины нити
для выбранного значения длины нити 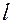 и рассчитать ускорение свободного падения по формуле
и рассчитать ускорение свободного падения по формуле
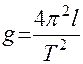 .
.
После оценки погрешности полученное значение 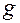 сравнивается с известным Вам табличным значением
сравнивается с известным Вам табличным значением 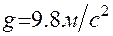 .
.
 2015-10-16
2015-10-16 1534
1534
