Опис лабораторної установки

Машина Атвуда (рис.1.2) складається з легкого блока, закріпленого на вертикальному стрижні та двох циліндрів однакової маси 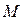, що з‘єднані ниткою, перекинутою через легкий блок.

Щодо установки, то будемо вважати, що

а) нитка невагома і не деформується;

б) блок невагомий;

в) сила тертя в блоці відсутня.

За цих умов сила натягу нитки 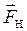ліворуч і праворуч від блока будуть однаковими.

Покладемо на правий циліндр тягарець масою 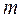<< 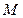. Правий і лівий циліндри почнуть рухатися з однаковим прискоренням у взаємно протилежних напрямках.

За другим законом Ньютона рівнодійна 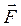сил, що діють на тіло, дорівнює добутку його маси m на прискорення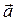

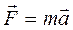. (2.5)

Застосуємо другий закон Ньютона для лівого циліндра. На циліндр діють сила натягу нитки 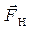, та сила тяжіння .

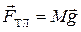Їх рівнодійна

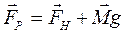. (2.6)

Тоді другий закон для лівого циліндра матиме вигляд в векторній формі

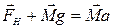. (2.7)

Враховуючи додатній напрямок осі 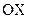(див. рис. 2.1), запишемо його в скалярній формі

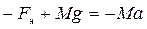. (2.8)

Застосуємо другий закон Ньютона для правого циліндра з тягарцем .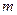

На циліндр діють сила натягу нитки 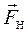та сила тяжіння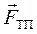

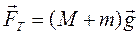. (2.9)

Їх рівнодійна буде

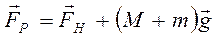(2.10)

Тоді другий закон Ньютона для правого циліндра матиме вигляд:

у векторній формі

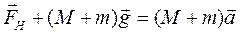(2.11)

в скалярній формі

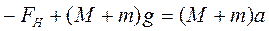(2.12)

Об’єднавши рівняння (2.8) та (2.12) маємо систему рівнянь

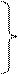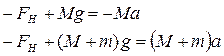
(2.13)

Розв‘язавши систему рівнянь одержимо величину прискорення а, з яким рухається вся система тягарців

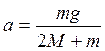. (2.14)

Враховуючи, що згідно другого закону Ньютона

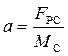, (2.15)

де 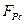- рівнодійна сила, що діє на систему масою М _С

Порівнявши рівняння (2.15) та (2.14) і врахувавши (2.17) можна стверджувати, що

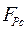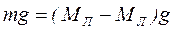= ; (2.16)

Маса системи

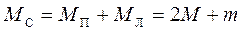, (2.17)

де 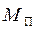– маса правої рухомої частини; 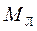– маса лівої частини.

Тому рівняння (2.14) набуває вигляду

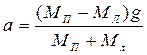; (2.18)

Якщо зафіксувати масу системи

,

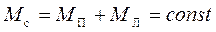а змінювати рівнодійну силу (див. формулу (2.16))

,

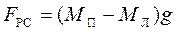то можна дослідити залежність прискорення 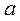від рівнодійної сили 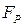і перевірити співвідношення

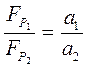. (2.19)

Якщо зафіксувати величину рівнодійної сили

,

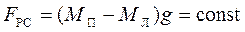а змінювати масу системи 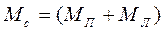, то можна дослідити залежність прискорення 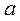від маси системи 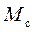та перевірити співвідношення

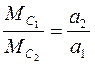(2.20)