Задание

1. Сбалансируйте маятник. Для этого оставьте на крестовине два груза на двух противоположных спицах на равных расстояниях от оси вращения. Спицы, на которых находятся грузы, соединены со втулкой резьбой. Вращая спицы в резьбе, добейтесь равновесия. Затем точно сбалансируйте грузы на второй паре спиц на таком же расстоянии от оси вращения.

Полезно несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. Подумайте, как на основании этих опытов определить, хорошо ли сбалансирован маятник.

2. Определите приближенно минимальную массу m₀, при которой маятник начинает вращаться, и оцените момент сил трения из соотношения M_тр≈m₀gr,

где r — радиус шкива, на котором подвешен груз m₀.

3. Оцените ускорение ε₀, возникающее под действием момента сил трения. Для этого приведите маятник во вращение, измерьте время T ₀, за которое он совершает первый оборот, и полное число оборотов маятника до полной остановки. Затем по формуле (15) вычислите ε₀. Измерения повторите три раза и сравните соответствующие им значения ε₀.

4. Определите экспериментально зависимость углового ускорения ε маятника от момента приложенной силы mgr. В этой серии измерений момент инерции маятника должен оставаться постоянным: I = const.

Для определения зависимости ε = ε (mgr) измерьте время t, за которое груз m опускается на расстояние h. Измерение времени t для каждого груза при постоянном значении h повторите три раза. Затем найдите среднее значение времени падения груза по формуле

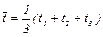
и определите среднее ускорение груза из соотношения (7):

.

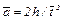Эти измерения и вычисления повторите для пяти значений массы m груза, причем для всех m должно выполняться неравенство m >> m₀, где m₀ — масса-перегрузка страгивающего маятник (см. п. 2).

Результаты измерений запишите в табл. 1.

Таблица 1

t1	t2	t3		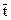	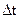h		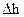		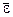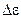mgr

r =

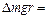
1. Время Δ t определяется из соотношения:

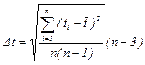
2. Угловое ускорение находится по формуле ε = а/r.

3. Δm определяется с точностью, с которой известна масса грузов m.

Полученные экспериментально точки отложите в координатной плоскости х=mgr, у =ε и по ним постройте график зависимости

(рис. 3, а).

5. Проверьте экспериментально зависимость (11). Для этого, взяв постоянную массу груза m >> m₀, определите ускорение а груза m при пяти различных положениях R на спицах грузов m_гр.

В каждом положении R измерения времени падения t груза m с высоты h повторите три раза. Результаты измерений занесите в табл. 2, где 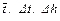определяются так же, как в табл. 1.

Полученные экспериментальные точки нанесите с учетом погрешностей в координатной плоскости х =(R/r)², у = g/ 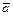и постройте график зависимости у = у (х) (рис. 3, б).

Таблица 2

R

r

(R/r)2

mгр

t1

t2

t3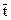

Δt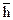

Δh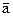

g/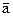

Задачи

1. Определить момент инерции сплошного шара массой m=10 кг и радиусом R=0,1 м относительно оси, проходящей через центр тяжести.

Ответы: 1) 0,25^.10^–2 кг^.м²; 2)1,32^.10^–2 кг^.м²; 3) 2,02^.10^–2 кг^.м²; 4) 0,04 кг^.м²; 5 5) 0,0431 кг^.м².

2. Цилиндр диаметром 12 см, имеющий массу 3 кг лежит боковой поверхностью на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта с плоскостью.

Ответы: 1) 0,0162 кг^.м²; 2) 0,0153 кг^.м²; 3) 0,0218 кг^.м²;

4) 0,0123 кг^.м²; 5) 0, 00923 кг^.м².

3. Определить момент инерции тонкого обода радиусом r=0,5м и массой 3 кг относительно оси, проходящей через центр тяжести.

Ответы: 1) 0.235 кг^.м²; 2) 1,25^.10^–2 кг^.м²; 3) 0,375 кг^.м²; 4) 0,575 кг^.м²;

5) 0,75 кг^.м²; 6) 2,65^.10^–2 кг^.м².

4. Диск радиусом 0,5 м и массой 20 кг вращается вокруг оси перпендикулярной плоскости диска и проходящей через его центр тяжести. Найти момент инерции диска относительно этой оси.

Ответы: 1) 0,250 кг^.м²; 2) 2,50 кг^.м²; 3) 0,125 кг^.м²; 4) 0,0135 кг^.м²; 5) 5,5 кг^.м².

5. Определить момент инерции вала массой 5 кг и радиусом R=0,02 м относительно оси, параллельной его оси симметрии и удаленной от нее на расстоянии а=10 см.

Ответы: 1) 0,135 кг^.м²; 2) 0,0310 кг^.м²; 3) 0,0235 кг^.м²; 4) 0,0510 кг^.м²; 5) 0,205 кг^.м².

6. Маховик вращается по закону, выраженному уравнением φ=А+Вt+Ct², где А=2 рад, В=–16 рад/с, С=–2 рад/с². Момент инерции колеса равен 50 кг^.м². Чему равен вращающий момент М?

Ответы: 1) –25 Нм; 2) 125 Нм; 3) 75 Нм; 4) –100 Нм; 5) 230 Нм.

Контрольные вопросы

1. Запишите основное уравнение динамики вращательного движения.

2. Устройство и принцип действия маятника Обербека.

3. Как используется теорема Гюйгенса–Штейнера в работе?

Литература

1. Сивухин Д. В. Общий курс физики. Т. 1. Механика. М., 1989.

2. Савельев И. В. Курс физики, т. 1. М., 1989.

3. Детлаф А. А., Яворский Б. М. Курс физики. М., 1989.

4. Каленков С. Г., Соломахо Г. И. Практикум по физике. М.: Высшая школа, 1990.

Лабораторная работа 1.17