Ускорение свободного падения g измеряется различными методами. В данной работе g определяется при помощи математического маятника. Математическим маятником называется материальная точка весом 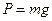 , подвешенная на гибкой, невесомой и нерастяжимой нити (рис. 1).
, подвешенная на гибкой, невесомой и нерастяжимой нити (рис. 1).
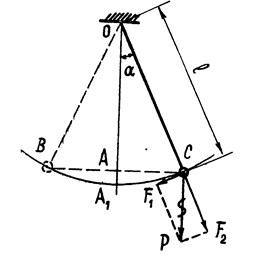
Рис. 10
В данном случае материальной точкой можно считать физическое тело с массой m, если его размерами можно пренебречь по сравнению с длиной подвеса. В вертикальном положении сила тяжести материальной точки
P полностью уравновешивается натяжением нити, и маятник остается в положении равновесия.
Если маятник отклонить от положения равновесия 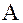 на некоторый угол
на некоторый угол 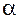 , то составляющая силы тяжести, направленная вдоль нити, т.е. сила
, то составляющая силы тяжести, направленная вдоль нити, т.е. сила 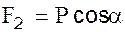 , уравновесится натяжением нити; другая же составляющая, т.е. сила
, уравновесится натяжением нити; другая же составляющая, т.е. сила 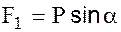 , перпендикулярная к нити, будет стремиться вернуть маятник в положение равновесия. Расстояние
, перпендикулярная к нити, будет стремиться вернуть маятник в положение равновесия. Расстояние 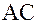 , на которое маятник отклонится от положения равновесия, называется смещением. Если смещение от
, на которое маятник отклонится от положения равновесия, называется смещением. Если смещение от 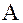 к
к 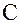 считать положительным, а от
считать положительным, а от 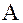 к
к 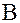 – отрицательным, то сила
– отрицательным, то сила 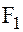 всегда будет направлена обратно смещению, и при малых углах (5° – 6°) пропорциональна смещению
всегда будет направлена обратно смещению, и при малых углах (5° – 6°) пропорциональна смещению 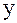 .
.
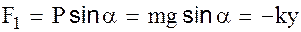 (1)
(1)
Согласно определению гармонического колебания, возвращающая сила прямо пропорциональна смещению и направлена к положению равновесия.

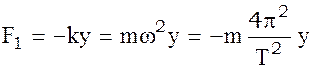 (2)
(2)
Где 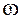 – круговая частота и
– круговая частота и 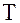 – период колебания.
– период колебания.
Считая, что при указанных выше ограничениях колебания маятника можно принять за гармонические, приравниваем выражения (1) и (2) и, учитывая, что
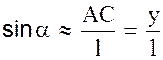 (4)
(4)
Напишем
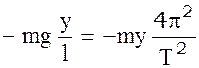 (4)
(4)
Решая (4) относительно периода колебаний математического маятника, получим:
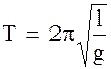 (5)
(5)
Формула (5) позволяет определить ускорение силы тяжести в данном географическом месте Земли, если известен период колебания математического маятника и его длина.
В лабораторных работах применяется маятник, подвешиваемый на двойной нити для того, чтобы колебания происходили по возможности в одной плоскости. Кроме этого, для устранения необходимости измерять строго сами длины маятников и диаметры шариков, применяют метод измерения двух периодов 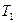 и
и 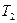 при разных длинах маятника
при разных длинах маятника
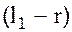 и
и 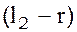 ,
,
где 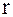 – радиус шарика маятника, а
– радиус шарика маятника, а 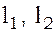 – длины подвеса маятников до нижней точки шариков (отсчёты по шкале).
– длины подвеса маятников до нижней точки шариков (отсчёты по шкале).
Напишем формулу (5) для этих двух случаев, предварительно возведя в квадрат обе части равенства
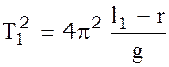 (6)
(6)
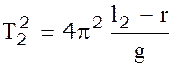 (7)
(7)
Вычитая почленно (7) из (6), получим:
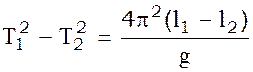 (8)
(8)
Откуда
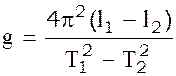 (9)
(9)
 2015-10-16
2015-10-16 267
267








