Метод измерения скорости полета снаряда основан на законе сохранения момента импульса относительно некоторой оси.
Моментом импульса материальной точки относительно некото-рого центра О называется векторная величина 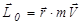 (
(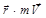 - векторное произведение вектора
- векторное произведение вектора 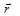 на вектор
на вектор 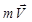 ), где
), где 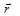 - радиус-вектор материальной точки, проведенный из центра О (рис. 8.1)
- радиус-вектор материальной точки, проведенный из центра О (рис. 8.1) 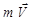 - импульс (количество движения) материальной точки. Численно
- импульс (количество движения) материальной точки. Численно 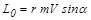 , где α – угол между векторами
, где α – угол между векторами 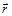 и
и 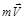 .
.
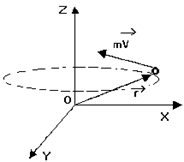 Рис.8.1
Рис.8.1
| Проекция вектора 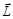 , на ось Z, проходящую через точку 0, называется моментом импульса материальной точки относительно оси Z, , на ось Z, проходящую через точку 0, называется моментом импульса материальной точки относительно оси Z, 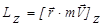
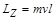 , где , где 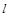 - кратчайшее расстояние от оси вращения до прямой, вдоль которой направлена скорость. - кратчайшее расстояние от оси вращения до прямой, вдоль которой направлена скорость.
|
Для твердого тела, вращавшегося вокруг неподвижной оси, момент импульса определяется выражением 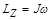 , где
, где 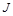 - момент инерции тела относительно оси вращения,
- момент инерции тела относительно оси вращения, 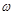 - угловая скорость вращения.
- угловая скорость вращения.
Момент импульса системы тел определяется выражением
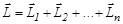 , (8.1)
, (8.1)
где 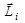 , - момент импульса i-го тела.
, - момент импульса i-го тела.
Закон сохранения момента импульса относительно некоторой оси формулируется следующим образом: если момент внешних сил, действующих на систему относительно некоторой оси равен нулю, то момент импульса системы по отношению к той же оси остается постоянным.
Пусть снаряд массой 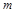 , движущийся со скоростью
, движущийся со скоростью 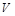 , попадает в неподвижное уравновешенное твердое тело на расстоянии
, попадает в неподвижное уравновешенное твердое тело на расстоянии 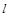 от оси вращения и застревает в нем. Применение закона сохранения момента импульса относительно оси вращения дает следующее соотношение
от оси вращения и застревает в нем. Применение закона сохранения момента импульса относительно оси вращения дает следующее соотношение
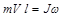 (8.2)
(8.2)
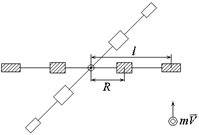 Рис. 8.2.
Рис. 8.2.
| До столкновения с телом моментом импульса обладал лишь снаряд 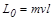 , после столкновения , после столкновения 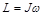 , где , где 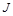 - момент инерции тела вместе со снарядом. По закону сохранения L0 = L.
Зная m, l, J, w можно определить скорость снаряда: - момент инерции тела вместе со снарядом. По закону сохранения L0 = L.
Зная m, l, J, w можно определить скорость снаряда:
|
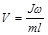 (8.3)
(8.3)
В настоящей работе для измерения скорости снаряда используется баллистический крутильный маятник ФРМ-09. Он состоит из основания, оснащенного регулируемыми ножками, которые позволяют устанавливать основание горизонтально. В основании закреплена стойка, на которой закреплены верхний, нижний и средний кронштейны. К среднему кронштейну прикреплено стреляющее устройство, а также прозрачный экран с нанесенной на него угловой шкалой и фотоэлектрический датчик. Кронштейны имеют зажимы, служащие для крепления стальной проволоки, на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином, двух перемещаемых грузов, двух стержней и водилки.
Сразу после соударения снаряда крутильный маятник обладает только кинетической энергией.
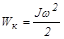 . (8.4)
. (8.4)
По достижении максимального отклонения из положения равновесия маятник останавливается, его кинетическая энергия переходит в потенциальную энергию упругой деформации закрученной проволоки
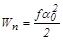 , (8.5)
, (8.5)
где f - модуль кручения проволоки; J - момент инерции маятника вместе со снарядом; w - наибольшее значение угловой скорости маятника; a0 - наибольший угол отклонения маятника из положения равновесия.
Приравнивая выражения (8.4) и (8.5) (по закону сохранения энергии) находим:
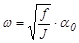 . (8.6)
. (8.6)
Тогда выражение (8.3) для скорости снаряда примет вид
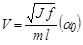 (8.7)
(8.7)
С другой стороны, движение маятника после попадания в него снаряда описывается основным законом динамки вращательного движения:
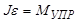 , (8.8)
, (8.8)
где 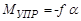 - момент сил упругости закрученной проволоки.
- момент сил упругости закрученной проволоки.
Так как угловое ускорение e - вторая производная от угла поворота a по времени, то мы приходим к дифференциальному уравнению колебательного движения маятника:
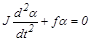 . (8.9)
. (8.9)
Решение этого уравнения ищут в виде:
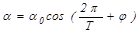 . (8.10)
. (8.10)
Выражение (8.10) будет удовлетворять уравнению (8.9) (в чем можно убедиться непосредственной подстановкой) лишь в том случае, когда
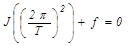 .
.
Откуда получается формула для периода колебаний крутильного маятника
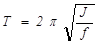 . (8.11)
. (8.11)
Подставляя в (8.7) выражение для момента инерции из (8.11), получим:
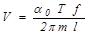 . (8.12)
. (8.12)
Специальная методика измерения скорости V позволяет исключить модуль кручения f из формулы (8.12).
Пусть снаряд был выпущен из стреляющего устройства, когда перемещаемые грузы находились на расстоянии R1 от оси вращения. В этом положении момент инерции маятника равен
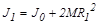 .
.
и период колебаний будет равен
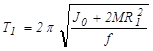 . (8.13)
. (8.13)
После перемещения грузов до расстояния 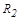 период изменится и станет равным
период изменится и станет равным
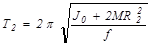 , (8.14)
, (8.14)
где J0 - момент инерции маятника без грузов; M - масса одного груза.
Из (8.13) и (8.14) можно получить следующее выражение для
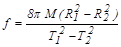 . (8.15)
. (8.15)
Подставляя выражение (8.15) в формулу (8.12) для 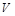 с учетом того, что T = T1, получим
с учетом того, что T = T1, получим
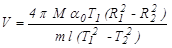 . (8.16)
. (8.16)
В формуле (8.16) величины M, m, l - задаются, а T1, T2, R1, R2, a0 - измеряются.
 2015-10-16
2015-10-16 315
315








