Основные понятия

ОПЕРАЦИОННОЕ ИССЧИСЛЕНИЕ

ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

Основные понятия

1. Оригинал – комплекснозначная функция f(t) действительного аргумента t, которая удовлетворяет следующим условиям:

а) f(t)=0 при t<0;

б) на любом конечном отрезке [a, b] 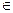[0, +∞) функция f(t) имеет не более чем конечное число точек разрыва первого рода;

в) f(t) имеет ограничительный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные М>0 и σ≥0, что

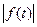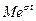< при t>0

Замечание 5.1.

1. Величина σ₀=inf σ называется показателем роста функции f(t). Для любой ограниченной функции, являющейся оригиналом, можно принять σ₀=0.

2. Обозначим

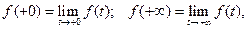
если пределы существуют и конечны.

3. Совокупность всех оригиналов называется пространством оригиналов.

4. В точке t₀ разрыва первого рода функция имеет конечное односторонние пределы: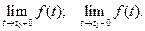

Пример 5.1. Проверить, являются ли функции

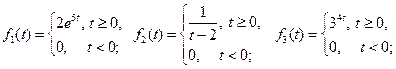
оригиналами.

Функция 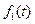является оригиналом, так как условия пп. «а»-«в» выполнены: М=2, σ₀=5; функция 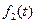не является оригиналом, так как в точке t=2 имеет разрыв второго рода (не выполняется условие «б»); функция 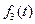не является оригиналом, так как растет быстрее показательной функции (не выполняется условие «в», поскольку 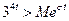для любых М и σ, t>0).

2. Изображение функции 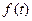- функция F(р) комплексного переменного р, определяемая равенством:

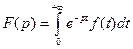(1)

Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (1). Исследование интеграла позволяет определить эту область и установить свойства функции F(р). Имеет место следующее утверждение.

Утверждение. Если функция 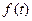, является оригиналом, то интеграл Лапласа сходится абсолютно в области Re p= σ> σ0 (рис. 1), где σ0 – показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве Re p= σ≥а> σ0, интеграл сходится равномерно и определяет аналитическую функцию F(р).

Замечания

1. Утверждение аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.

2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.

3. Совокупность всех изображений F(р) называется пространством изображений.

3. Переход, определяющий изображение F(р) по оригиналу 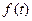, называется преобразованием Лапласа:

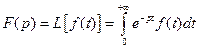(2)

Запись 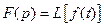означает, что оригиналу 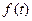соответствует изображение F(р).

4. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения

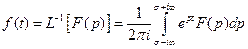(3)

Где путь интегрирования - любая прямая Re р=σ, параллельная мнимой оси лежащая правее прямой Rep =σ₀ (Рис.1).

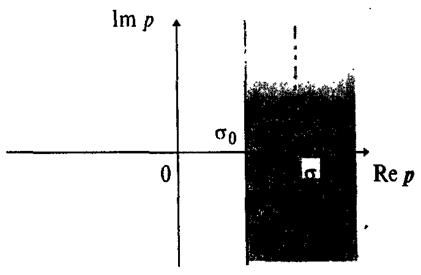
Рис. 1

1. Для преобразования Лапласа используются различные обозначения, например 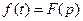и 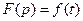, что означает: оригиналу 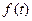соответствует изображение 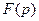и изображению 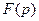соответствует оригинал 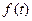. Вместо аргумента р применяется s, т.е. 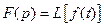и .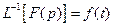

2. Для компактной записи оригиналов используется единичная ступенчатая функция :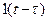

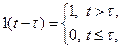(4)

Где 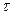- точка приложения (рис. 2). Так как во многих практических задачах аргумент t имеет смысл текущего времени, то 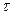также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция 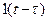рассматривается как типовой входной сигнал.

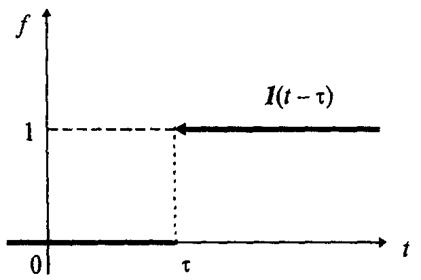
Рис. 2

При 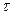=0 функция 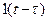является функцией Хевисайда:

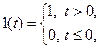(5)

Тогда, если функция f(t) удовлетворяет условиям "б", "в" в определении оригинала (п. 1), но не удовлетворяет условию "а", то функция 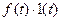будет оригиналом, так как

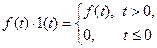
Далее под заданной с помощью аналитической формулы функцией f(t), там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель 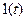опускать.

3. Функции F(p), являющиеся изображениями, удовлетворяют необходимому условию: если F(p) есть изображение, то F(p)→0 при Re р=σ→+∞.

Поэтому функции 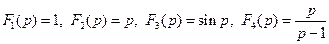не являются изображением. Однако в практических задачах функции типа 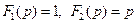и другие встречаются. Это требует расширения понятий оригинала и изображения.

Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости Re p> σ₀.