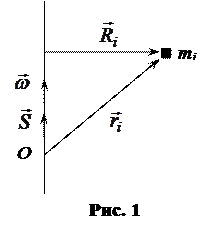 При описании вращательного движения твердого тела часто появляется необходимость знать его движение около точки закрепления. Важнейшим понятием при этом является тензор инерции. Для упрощения расчетов воспользуемся представлением о теле как совокупности материальных точек с массами
При описании вращательного движения твердого тела часто появляется необходимость знать его движение около точки закрепления. Важнейшим понятием при этом является тензор инерции. Для упрощения расчетов воспользуемся представлением о теле как совокупности материальных точек с массами 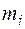 .
.
Закрепим тело в точке 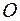 . Радиус-вектор точки с массой
. Радиус-вектор точки с массой 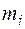 относительно
относительно 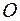 обозначим
обозначим 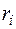 (см. рис. 1). Пусть
(см. рис. 1). Пусть 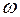 - мгновенная угловая скорость тела. Тогда скорость
- мгновенная угловая скорость тела. Тогда скорость 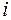 - й точки тела
- й точки тела 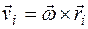 . Поэтому момент импульса
. Поэтому момент импульса 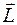 всего тела относительно точки
всего тела относительно точки 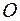 равен:
равен:
|
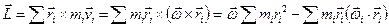 . (1)
. (1) где использована формула разложения двойного векторного произведения 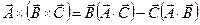 .
.
Векторное равенство (1) можно написать в виде трех проекций на оси координат:
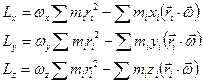 . (2)
. (2)
Учитывая, что 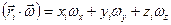 , вместо (2) имеем
, вместо (2) имеем
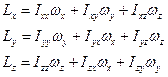 . (3)
. (3)
где:
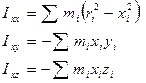 . (3а)
. (3а)
аналогично выражаются другие величины 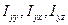 и т.д. Поэтому из 9 величин
и т.д. Поэтому из 9 величин 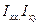 , различны лишь 6. Величины
, различны лишь 6. Величины 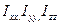 называются осевыми моментами инерции, а
называются осевыми моментами инерции, а 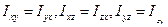 называются центробежными моментами инерции. Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле, и его направление не всегда совпадает, с угловой скоростью вращения тела. Совокупность величин
называются центробежными моментами инерции. Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле, и его направление не всегда совпадает, с угловой скоростью вращения тела. Совокупность величин
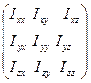 . (4)
. (4)
называется тензором инерции. Величины 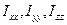 являются диагональными элементами тензора, а остальные – недиагональными. Если величины, расположенные симметрично относительно диагонали, равны, то такой тензор называется симметричным.
являются диагональными элементами тензора, а остальные – недиагональными. Если величины, расположенные симметрично относительно диагонали, равны, то такой тензор называется симметричным.
 2015-10-16
2015-10-16 4387
4387








