Известно, что момент импульса относительно оси, проходящей через центр масс, можно записать так:
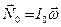 , (8)
, (8)
где 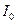 - тензор момента инерции относительно системы координат, начало которой совпадает с центром масс. Компоненты
- тензор момента инерции относительно системы координат, начало которой совпадает с центром масс. Компоненты 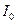 будут постоянны во времени, если система координат неизменно связана с телом.
будут постоянны во времени, если система координат неизменно связана с телом.
Зная 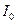 , можно найти момент инерции относительно любой оси, проходящей через
, можно найти момент инерции относительно любой оси, проходящей через 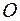 - центр масс тела. Пусть направление оси вращения задано вектором
- центр масс тела. Пусть направление оси вращения задано вектором 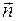 . Тогда, учитывая, что
. Тогда, учитывая, что 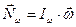 , по формуле (8) проекцию
, по формуле (8) проекцию 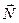 на
на 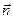 можно записать так:
можно записать так: 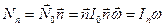 , где
, где 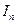 - момент инерции относительно оси
- момент инерции относительно оси 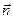 . Или:
. Или: 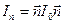 . Если записать число
. Если записать число 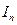 через компоненты тензора I0 и вектора
через компоненты тензора I0 и вектора 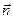 , то получим довольно громоздкое выражение. Приведем более краткую и ясную формулу, приняв за оси координат главные направления
, то получим довольно громоздкое выражение. Приведем более краткую и ясную формулу, приняв за оси координат главные направления 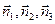 ; тогда
; тогда 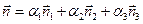 , где
, где 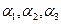 – направляющие косинусы
– направляющие косинусы 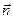 по отношению к осям
по отношению к осям 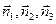 . Следовательно:
. Следовательно:
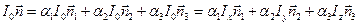 .
.
Поэтому: 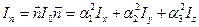 . (9)
. (9)
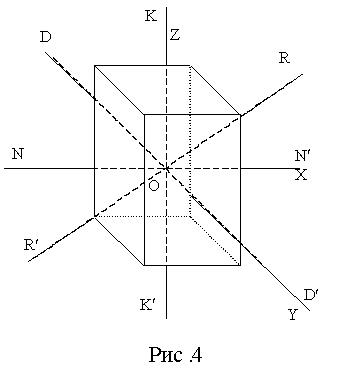 где
где 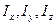 – моменты инерции относительно главных осей, проходящих через центр масс. По формуле (9) можем при известных
– моменты инерции относительно главных осей, проходящих через центр масс. По формуле (9) можем при известных 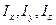 и
и 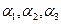 точно определить момент инерции
точно определить момент инерции 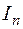 относительно любой оси
относительно любой оси 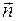 .
.
 2015-10-16
2015-10-16 796
796








