Определение угловой скорости маятника

Кинетическая энергия вращательного движения маятника 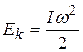, где 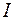- момент инерции маятника с грузами, переходит в потенциальную энергию, равную работе по закручиванию нити. Найдем её величину. Используя закона Гука, упругий момент нити M пропорционален углу поворота a маятника: 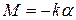. (3)

где 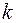- постоянная момента упругих сил.

Элементарная работа против сил упругости по закручиванию нити на угол 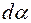равна 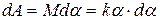. После интегрирования обеих частей равенства имеем: 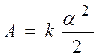. (4)

Закон сохранения механической энергии в этом случае запишется в виде:

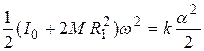. (5)

где 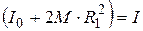. Из выражения (5) получим:

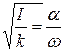, (6)

где 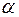- наибольший угол поворота маятника.

Используя основной закон динамики вращательного движения твердого тела: 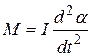. (7)

с учетом выражения (3) можно записать уравнение колебаний баллистического маятника в виде:

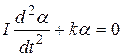. (8)

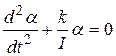или . (9)

Частным решением этого уравнения является: 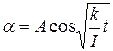, где величина 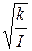- есть круговая частота 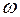, которая по определению равна 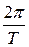. Таким образом, маятник будет совершать гармонические колебания с периодом:

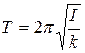. (10)

Заменяя в формуле (10) величину 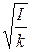ее значен6ием из выражения (6), получим 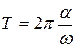, откуда искомая начальная угловая скорость маятника равна:

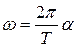. (11)