Важным примером практического применения физических маятников является так называемый оборотный маятник, служащий преимущественно для гравиметрической разведки, определения ускорения свободного падения в данной точке земной поверхности. Для достижения этой цели в процессе эксперимента маятник закрепляют так, чтобы его центр качания стал новой точкой подвеса и снова измеряют период колебаний. Если периоды колебаний маятника в обоих случаях одинаковы, значит равны и приведённые длины маятников в обоих случаях. Техника измерения длин высока, поэтому, измеряя расстояние между точками подвеса в двух положениях маятника, можно с высокой степенью точности определить приведенную длину маятника, и измерив период само значение ускорения свободного падения:
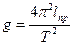
Для определения ускорения свободного падения можно было бы, конечно, применить и математический маятник. Но приближения, которые мы применяем, считая физический маятник математическим, не могут обеспечить достаточно высокую точность измерений. Кроме того, в эксперименте весьма затруднительно определить положение центра масс тела маятника и расстояние до него от точки подвеса. Всё это приводит к тому, что для точных определений ускорения свободного падения необходимо считать маятник физическим, а это приводит к дополнительным трудностям.
Очень важным, с точки зрения гравиметрических измерения, является следующее свойство физического маятника: если заставить маятник колебаться относительно центра качания, то прежняя точка подвеса станет новым центром качания, иначе говоря, центр качания и точка подвеса обладают свойством сопряженности.
Определить положение центра качания расчётным путём затруднительно в реальных условиях эксперимента, соответственно, трудно с достаточной степенью точности определить приведённую длину маятника. Но, пользуясь указанным свойством физического маятника, можно очень точно определить расстояние между двумя точками маятника, периоды колебаний относительно которых равны между собой, т.е. определить приведённую длину. Докажем теперь, что если подвесить маятник в центре качания, то прежняя точка подвеса станет новым центром качания, т.е. приведённая длина маятника не изменится.
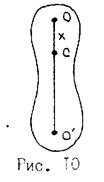
Для доказательства рассмотрим физический маятник произвольной формы, представленный на рис.90. Здесь О - точка подвеса, С - центр масс, O`- центр качания маятника, x - расстояние между точкой подвеса и центром масс маятника.
Если маятник подвешен в О, то приведённая длина его будет равна:
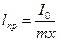
При повороте маятника и накоплении его в т. О' приведённая длина становится:
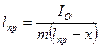
По теореме Гюйгенса-Штейнера момент инерции маятника относительно оси, проходящей через О`, можно записать в виде 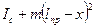 . С учётом этого приведённая длина маятника в случае, когда О` становится точкой подвеса, равна:
. С учётом этого приведённая длина маятника в случае, когда О` становится точкой подвеса, равна:
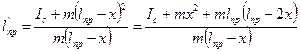
После несложных преобразований получаем, чть приведённая длина маятника одинакова в тех случаях, когда маятник колеблется относительно точек О' и О, т.е. приведённая длина не изменяется:
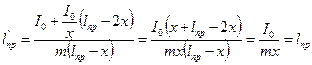
измерив расстояние между точками подвеса маятника, для которых период принимает одинаковое значение, и измерив само значение периода колебаний, определим затем и ускорение свободного падения.
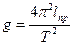
16.10. Циклоидальный маятник.
Математический и физический маятники имеют циклическую частоту и период, не зависящие от амплитуды колебаний только в том случае, когда амплитуда колебаний достаточно мала. С увеличением амплитуды колебаний они перестают быть, с одной стороны, гармоническими и, с другой стороны, их период будет уже зависеть от величины амплитуды. Однако, изменяя соответствующим образом параметры маятника, например, длину математического маятника, можно добиться того, что и при больших значениях амплитуды колебаний период колебаний не будет зависеть от её значения. Таким является так называемый циклоидальный маятник. Циклоидальным называют обычно математический маятник, у которого тело движется под действием силы тяжести по дуге циклоиды, ось которой вертикальна, а выпуклость обращена вниз. Период колебаний циклоидального маятника не зависит от амплитуды и определяется формулой
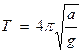 (336)
(336)
Таким образом, для циклоидального маятника строго выполняется свойство изохронности колебаний. На рис. 91 приведена разновидность циклоидального маятника, отличающаяся от приведенного его определения тем, что нить математического маятника при его колебаниях касается циклоиды, т.е. длина математического маятника с ростом отклонения тела от положения равновесия уменьшается на соответствующую дугу циклоиды.
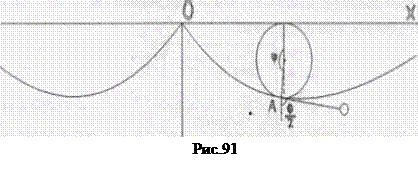 |
Положим, что радиус круга, образующего циклоиду, равен а, а длина маятника 4a. Уравнение циклоиды тогда можно записать в виде
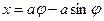
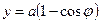
где угол 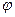 показан на рис.91.
показан на рис.91.
При колебаниях маятника в любой момент времени его длина уменьшается на величину дуги циклоиды, которой в этот момент времени касается нить маятника. Нить направлена по касательной к циклоиде в т. А. Тангенс угла отклонения нити от положительного направления оси ОХ легко определяется из выражения:
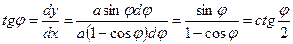
Отсюда видно, что угол отклонения нити маятника от вертикали равен 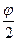 , длина дуги циклоиды ОА равна
, длина дуги циклоиды ОА равна 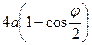 , а длина нити маятника в этот момент времени, соответственно,
, а длина нити маятника в этот момент времени, соответственно, 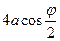 .
.
Предположим далее, что колебания маятника возбуждаются толчком, т.е. ему сообщается кинетическая энергия. При максимальном отклонении тела маятника от положения равновесия при отсутствии сил сопротивления движению энергия его полностью переходит в потенциальную энергию в поле тяготения, т.е. 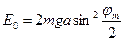 ,где Е0- -начальная энергия,
,где Е0- -начальная энергия, 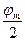 - угол максимального отклонения маятника.
- угол максимального отклонения маятника.
В произвольный момент времени полная энергия маятника (см. "Энергия колебательного движения") состоит из кинетической энергии движения и потенциальной энергии в поле силы тяжести: 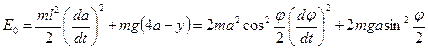
Из полученного выражения для закона сохранения энергии получим значение угловой скорости маятника для произвольного момента времени
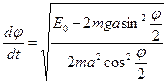
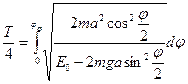 |
Последнее выражение позволяет определить период колебаний маятника. Действительно, время движения маятника от положения равновесия до максимального отклонения равно четверти периода, поэтому
Выражение интеграла можно привести к более удобному для интегрирования виду, учитывая значение кинетической энергии, сообщённой маятнику
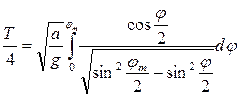 |
Если применить подстановку 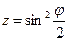 интеграл приводится к табличному
интеграл приводится к табличному
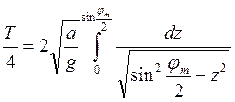
После интегрирования получаем
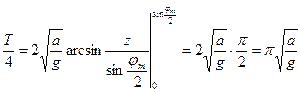
Следовательно, период колебаний циклоидального маятника совершенно не зависит от амплитуды колебаний, т.е. свойство изохронности колебаний выполняется строго. Значение периода колебаний будет определяться только параметрами самой циклоиды (радиусом круга, образующего циклоиду):
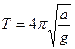
 2015-05-13
2015-05-13 7694
7694
