2015-10-16
1007
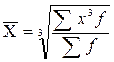
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Более используется в статистике средняя квадратическая, но не из самих вариантов x, а из их отклонений от средней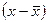 
при расчете показателей вариации.
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. Это мода и медиана.
Мода (Мо) – значение признака, наиболее часто встречающееся в совокупности, т.е. варианта, имеющая наибольшую частоту.
Например, имеются следующие данные по бригаде:
| Выработка деталей за смену одним рабочим, шт. | Число рабочих |
| Итого |
В данном случае модальное значение выработки равно 20 деталей, т.к. ему соответствует наибольшая частота f = 5.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
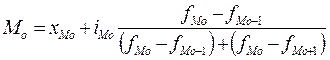, где
х Мо – нижняя граница модального интервала
i Мо – величина модального интервала
f Мо – частота модального интервала
f Мо-1 – частота интервала, стоящего перед модальным
f Мо+1 – частота интервала, следующего за модальным
Модальный интервал – это интервал, которому соответствует наибольшая частота f.
Например, имеются данные по предприятиям региона:
| Группы предприятий по стоимости основных фондов, млн. руб | Число предприятий |
| 14-16 | |
| 16-18 | |
| 18-20 | |
| 20-22 | |
| 22-24 | |
| Итого |
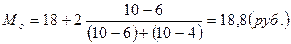
Модальным значением стоимости основных фондов предприятий региона является стоимость равная 18,8 млн. руб.
Медиана (Ме) – это варианта, находящаяся в середине ранжированного вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.
Если вариационный дискретный ряд нечетный, то номер медианы вычисляется по формуле:
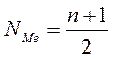, где n – число членов ряда.
Например, имеются данные по бригаде:
| Табельный № рабочего | Выработка за месяц, тыс. руб |
Ранжируем выработку по возрастанию признака:
| № по ранжиру | |||||||
| Выработка, тыс. руб. |
Определяем номер медианового показателя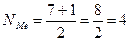 
, таким образом, медиана равна 690 тыс. руб., т.е. одна половина рабочих бригады имела выработку менее 690 тыс. руб., а другая – более 690 тыс. руб.
В случае четного вариационного дискретного ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
Например, имеется заработная плата по 8 рабочим завода:
| Табельный номер | Зарплата, тыс. руб. |
| 5,3 | |
| 4,8 | |
| 5,2 | |
| 5,0 | |
| 5,5 | |
| 6,0 | |
| 4,9 | |
| 5,5 |
Проранжируем ряд по возрастанию зарплаты:
| Номер по ранжиру | Зарплата, тыс. руб. |
| 4,8 | |
| 4,9 | |
| 5,0 | |
| 5,2 | |
| 5,3 | |
| 5,5 | |
| 5,5 | |
| 6,0 |
В середине стоят 4 и 5 рабочие по ранжиру, значит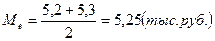 
Медианная зарплата равна 5,25 тыс. руб.
В интервальных рядах распределения медианное значение (поскольку оно делит совокупность на две равные по численности части) оказывается в каком-то из интервалов. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется по формуле:
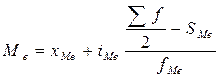, где
х Ме – нижняя граница медианного интервала
i Ме – медианный интервал
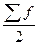- полусумма всех частот ряда
S Ме – сумма частот интервалов, стоящих перед медианным
fМе – частота медианного интервала
Например, имеются данные по предприятиям региона:
| Группы предприятий по стоимости основных фондов, млн. руб. | Число предприятий |
| 14-16 | |
| 16-18 | |
| 18-20 | |
| 20-22 | |
| 22-24 | |
| Итого |
Прежде всего найдем медианный интервал, 
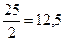, т.е. медианное значение будет средним из значений у 12-го и 13-го предприятий в ранжированном ряду. Очевидно, что эти предприятия находятся в третьем интервале (18-20 млн. руб.), поскольку его кумулятивная частота равна 18(2+6+10), что превышает половину суммы всех частот ().
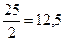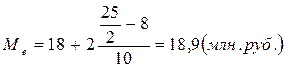
Из 25 предприятий региона 12 предприятий имеют стоимость основных фондов менее 18 млн. руб., а 12 предприятий – более 18 млн. руб.
