Показатели вариации

Вариация – это различие в значениях какого – либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Например работники СХПК различаются по доходам, затратам времени на работу, росту, весу, образованию, профессии и т.д.

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строение совокупности, не показывает, как располагаются около нее варианты осредняемого признака. Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, - чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Поэтому возникает необходимость измерять вариацию признака в совокупностях с помощью ряда обобщающих показателей. К ним относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

Размах вариации R – разность между максимальным и минимальным значениями признака

R = Xmax - Xmin

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариант в ряду. Для более точного анализа вариации необходимы показатели, которые отражают все колебания варьирующего признака и дают обобщенную характеристику. Простейший из показателей такого типа – среднее линейное отклонение 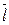. Оно определяется как среднее арифметическое из отклонений индивидуальных значений от средней без учета знака этих отклонений.

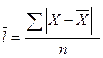или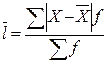

Среднее линейное отклонение как меру вариации признака применяют в статистической практике в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл (например, анализ состава работающих, ритмичность производства, оборот внешней торговли).

Дисперсия 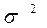в зависимости от исходных данных вычисляется по формулам простой и взвешенной.

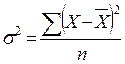или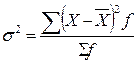

Дисперсия представляет собой средний квадрат отклонений вариантов от их средней величины.

Среднее квадратическое отклонение 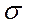равно корню квадратному из дисперсии. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем качественно однороднее совокупность и тем более типичной будет средняя величина.

Для сравнения вариаций различных признаков, а также колеблемости одного и того же признака в нескольких совокупностях используют относительный показатель вариации – коэффициент вариации V.

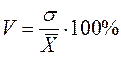
Коэффициент вариации характеризует, на сколько процентов в среднем отклоняются индивидуальные показатели от их среднего значения.

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

Например, имеются данные о сменной выработке рабочих бригады, которые представлены интервальным рядов распределения:

Группы рабочих по сменной выработке изделий, шт.	Число рабо- чих f	Середина интервала x	Расчетные значения
X f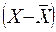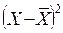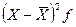
170-190				-36
190-210				-16
210-230
230-250
Итого		X		X	X

Исчислим среднюю выработку на одного работника:

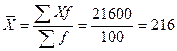(шт.)

Среднеквадратическое отклонение:

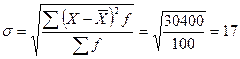(шт.)

Коэффициент вариации:

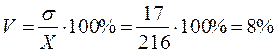
Таким образом, индивидуальные выработки рабочих за смену колеблются вокруг средней выработки в среднем на 216 изделий или 8%. Данная бригада рабочих по выработке достаточно однородна, поскольку вариация признака составляет лишь 8%, что меньше 33%.

Вариация признака обусловлена различными факторами. Определить их влияние на колеблемость индивидуальных значений признака можно при помощи трех видов дисперсий:

1) общей дисперсии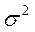

2) межгрупповой дисперсии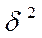

3) средней из внутригрупповых дисперсий

Общая дисперсия 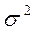измеряет вариацию признакапо всейсовокупности под влиянием всех факторов, обусловивших эту вариацию. Она может быть вычислена по простой или взвешенной формуле:

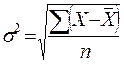или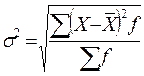

Межгрупповая дисперсия 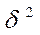характеризует систематическую вариацию результативного признака, обусловленную влиянием факторного признака, положенного в основу группировки.

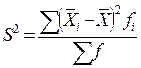,т.е. она равна среднему квадрату отклонений групповых средних 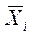от общей средней по всей совокупности .

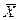Внутригрупповая дисперсия 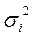отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от группировочного признака. Она исчисляется внутри каждой группы:

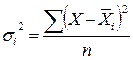или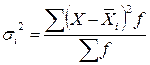

На основании внутригрупповых дисперсий вычисляют среднюю из внутригрупповых дисперсий:

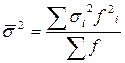
Согласно правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий, т.е.

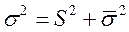
Например, при изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в таблице:

NN п/п	Рабочие 4-го разряда	N п/п	Рабочие 5-го разряда
Выработка, шт.	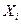		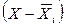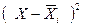Выработка, шт.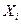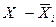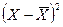
		-3				-1
		-1				-1
		-1
						-2
Итог		X				X

Результативный признак – выработка рабочего – варьирует под влиянием факторного признака (квалификации), а также под влиянием других неучтенных случайных факторных признаков. Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповых.

1. Для расчета групповых дисперсий исчислим средние выработки по каждой группе и общую среднюю выработку, шт.:

по первой группе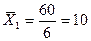

по второй группе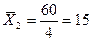

в целом по десяти рабочим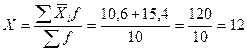

2.Исчислим общую дисперсию по формуле

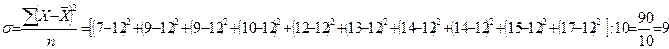
Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию выработки изделий в среднем рабочими цеха.

3. Исчислим межгрупповую дисперсию

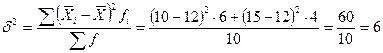
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду.

4. Данные для расчета внутригрупповых дисперсий представлены в таблице.

Внутригрупповые дисперсии

- по первой группе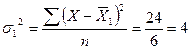

- по второй группе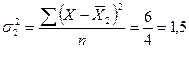

Средняя из внутригрупповых дисперсий:

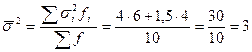
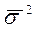отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих.

5. Проверим правило сложения дисперсий:

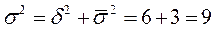
Очевидно, чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного признака (квалификационного разряда) на результативный признак (количество изделий на рабочего).

Для определения этой доли используется эмпирический коэффициент детерминации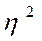

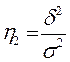
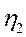показывает долю вариации результативного признака под влиянием факторного признака.

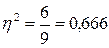или 66,6%

Это означает, что на 66,6% вариация производительности труда рабочих обусловлена различиями в их квалификации и на 33,4% (100% - 66,6% = 33,4%) – влиянием прочих факторов.

ТЕМА: «ВЫБОРОЧНЫЙ МЕТОД»

1. Понятие о выборочном наблюдении

Выборочное наблюдение представляет собой такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, далее отобранная часть изучается, а затем результаты распространяются на всю исходную совокупность. Наблюдение осуществляется таким образом, что эта часть отобранных единиц представляет всю совокупность с достаточной для практике степенью точности.

Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели – генеральными.

Выборочная совокупность – это совокупность единиц, отобранных из генеральной совокупности. Все ее обобщающие показатели называются выборочными.

Основными причинами, по которым во многих случаях выборочному наблюдению отдается предпочтение перед сплошным, являются:

1. экономия материальных, трудовых, финансовых ресурсов и времени в результате сокращения объема работы;
2. сведения к минимуму порчи или уничтожения исследуемых объектов;
3. необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (например, при изучении бюджета домохозяйств);
4. достижение достаточно большой точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.

Преимущество выборочного наблюдения по сравнению со сплошным можно реализовать, если оно организовано и приведено в соответствии с научными принципами теории выборочного метода. Это обеспечение случайности, т. е. равной возможности попадания в выборку единиц генеральной совокупности, и достаточного числа единиц отбора.

Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (т.е. средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических исследованиях (сплошных и выборочных) возникают ошибки.

Ошибки регистрации могут возникать и при сплошных, и при выборочных наблюдениях. Они могут иметь случайный (непреднамеренный) и систематический (преднамеренный) характер.

Ошибки репрезентативности (представительности) присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенной с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборочных и генеральных характеристик.

Ошибки репрезентативности возникают вследствие двух причин:

1) из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки)

2) в результате самого отбора (случайные ошибки)

Систематические ошибки выборки устраняются. Случайные ошибки устранить нельзя, но их рассчитывают и учитывают при переносе выборочных характеристик на генеральную совокупность.

Случайные ошибки репрезентативности бывают средними (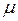) и предельными ().

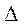Средняя ошибка выборки представляет собой такое расхождение между средними выборочной и генеральной совокупностей, которое не превышает среднеквадратическое отклонение в выборке.

Предельной ошибкой называется максимальное расхождение средних характеристик выборочной и генеральной совокупностей при заданной вероятности появления этой ошибки.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами вновь попасть в выборку.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует.

По степени охвата единиц совокупности различают большие и малые (n < 30) выборки.

В практике выборочных исследований наибольшее распространение получили следующие виды выборки: простая случайная (собственно - случайная), механическая, типическая, серийная, комбинированная и др.

Основные характеристики параметров генеральной и выборочной совокупности обозначаются символами:

N – объем генеральной совокупности (количество единиц, входящих в генеральную совокупность)

n – объем выборочной совокупности (количество единиц, входящих в выборочную совокупность)

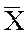- генеральная средняя (среднее значение признака в генеральной совокупности)

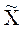- выборочная средняя (среднее значение признака в выборочной совокупности)

P – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

W – выборочная доля (доля, единиц обладающих данным признаком в выборочной совокупности)

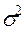- генеральная дисперсия (дисперсия признака в генеральной совокупности)

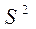- выборочная дисперсия (дисперсия признака в выборочной совокупности)

t – коэффициент доверия при заданном уровне вероятности P