Задача 1. Для изготовления изделий типа А и В используется сырье трех видов, запасы каждого из которых 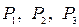 . На производство одного изделия типа А требуется затратить
. На производство одного изделия типа А требуется затратить 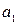 кг сырья первого вида,
кг сырья первого вида, 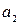 кг сырья второго вида,
кг сырья второго вида, 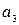 кг сырья третьего вида. На одно изделие типа В расходуется соответственно
кг сырья третьего вида. На одно изделие типа В расходуется соответственно 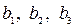 кг сырья каждого вида. Прибыль от реализации единицы изделия А составляет
кг сырья каждого вида. Прибыль от реализации единицы изделия А составляет 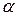 (ден. ед.), а изделия В -
(ден. ед.), а изделия В - 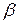 (ден. ед.). Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом, а также дать геометрическое истолкование задачи. Все данные приведены в следующей таблице:
(ден. ед.). Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом, а также дать геометрическое истолкование задачи. Все данные приведены в следующей таблице:
| № Варианта | Изделие типа А | Изделие типа В | Запасы сырья | ||||||||
| Затраты сырья на 1 кг изделия | Цена 1 изделия | Затраты сырья на 1 кг изделия | Цена 1 изделия | 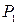 | 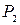 | 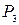 | |||||
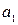 | 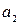 | 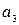 | 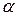 | 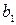 | 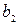 | 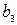 | 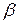 | ||||
Задача 2. Задана каноническая модель задачи линейного программирования:
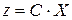 ,
, 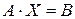 ,
, 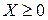 ,
, 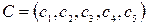 ,
, 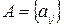 .
.
Требуется найти симплекс-методом с искусственным базисом (М-методом) план, обеспечивающий 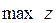 .
.
1. 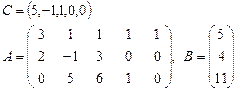 2.
2. 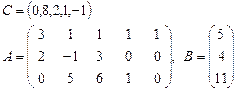
3. 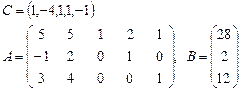 4.
4. 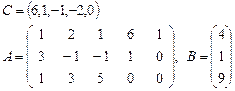
5. 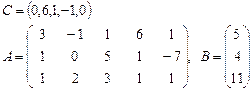 6.
6. 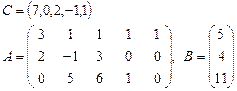
7. 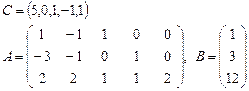 8.
8. 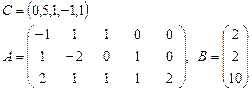
9. 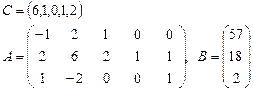 10.
10. 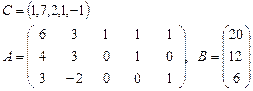
11. 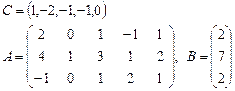 12.
12. 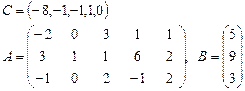
13. 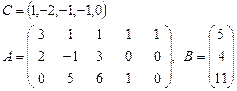 14.
14. 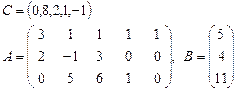
15. 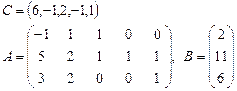 16.
16. 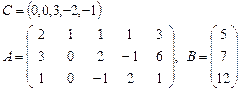
17. 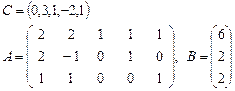 18.
18. 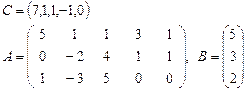
19. 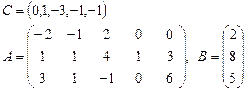 20.
20. 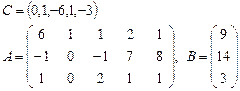
21. 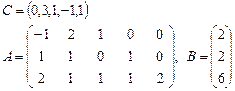 22.
22. 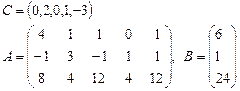
23. 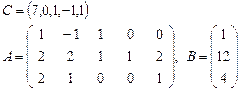 24.
24. 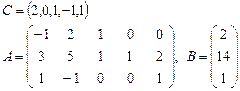
25. 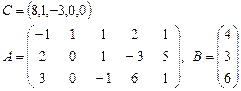 26.
26. 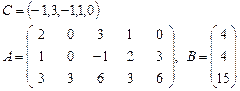
Задача 3. Имеются 3 пункта поставки однородного груза 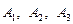 и 5 пунктов потребления
и 5 пунктов потребления 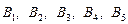 . На пунктах
. На пунктах 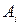
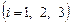 груз находится соответственно в количествах
груз находится соответственно в количествах 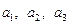 условных единиц. В пункты
условных единиц. В пункты 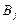
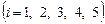 требуется доставить соответственно
требуется доставить соответственно 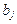 единиц груза. Стоимость перевозки единицы груза (с учетом расстояний) из
единиц груза. Стоимость перевозки единицы груза (с учетом расстояний) из 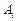 в
в 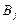 определена матрицей
определена матрицей 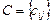 . Требуется найти план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальны.
. Требуется найти план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальны.
1. 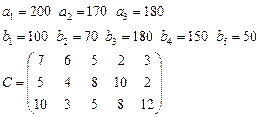 2.
2. 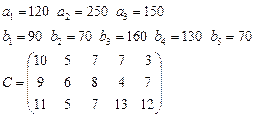
3. 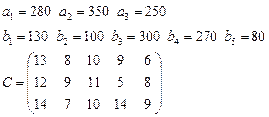 4.
4. 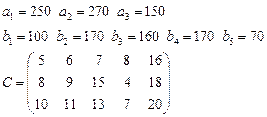
5. 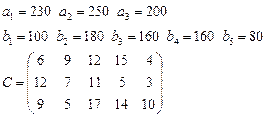 6.
6. 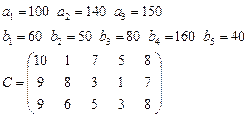
7. 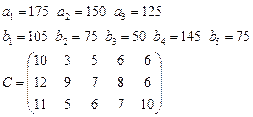 8.
8. 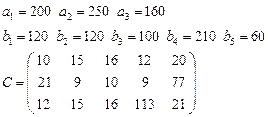
9. 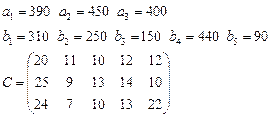 10.
10. 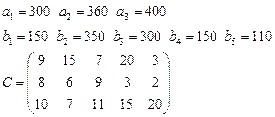
11. 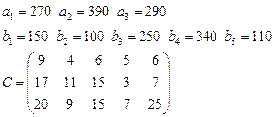 12.
12. 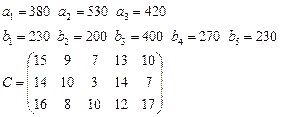
13. 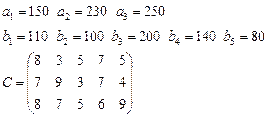 14.
14. 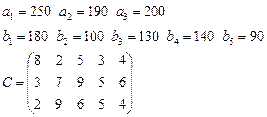
15. 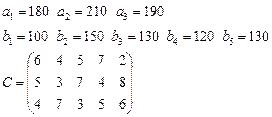 16.
16. 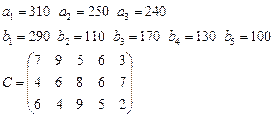
17. 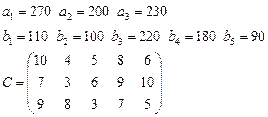 18.
18. 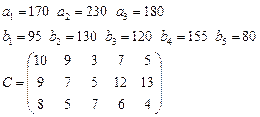
19. 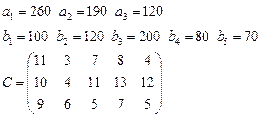 20.
20. 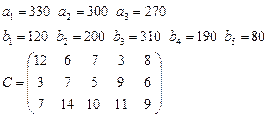
21. 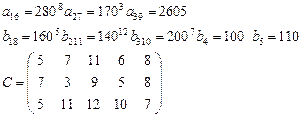 22.
22. 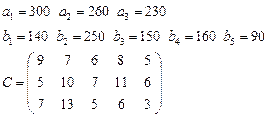
23. 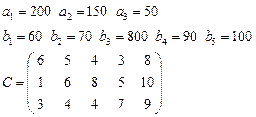 24.
24. 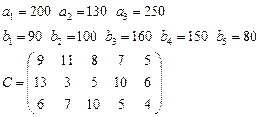
25. 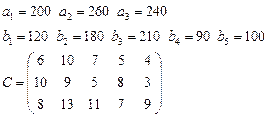
Задача 4. В клетках таблицы даны тарифы перевозок единицы груза из пункта 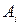
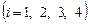 в пункт
в пункт 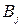
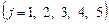 .
.
Требуется составить план, обеспечивающий минимальные суммарные затраты на перевозку товаров при следующих ограничениях:
§ если спрос превосходит предложение, то полностью удовлетворить потребности пункта 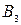 ; если же предложение превосходит спрос, то исчерпать полностью запасы пункта
; если же предложение превосходит спрос, то исчерпать полностью запасы пункта 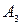 ;
;
§ заблокировать перевозки из 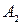 в
в 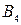 .
.
1. 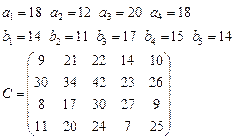 2.
2. 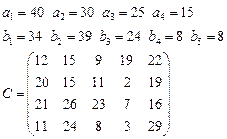
3. 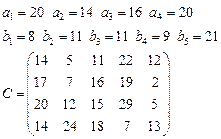 4.
4. 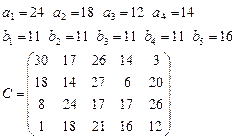
5. 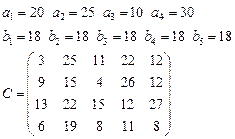 6.
6. 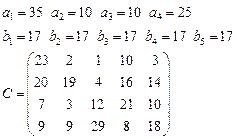
7. 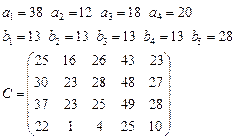 8.
8. 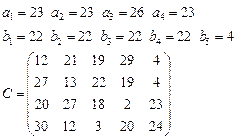
9.  10.
10. 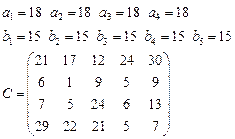
11. 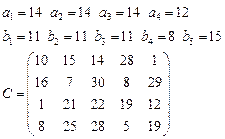 12.
12. 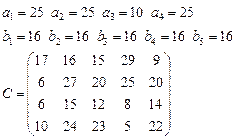
13. 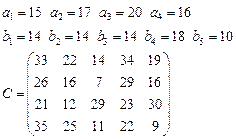 14.
14. 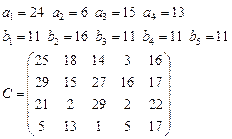
15. 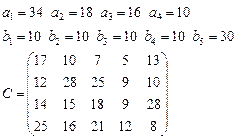 16.
16. 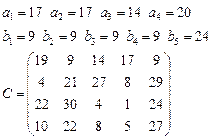
17. 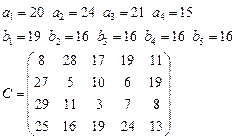 18.
18. 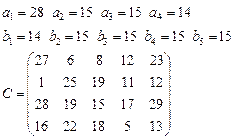
19. 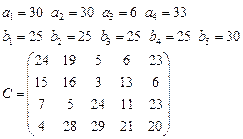 20.
20. 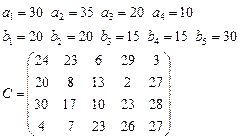
21. 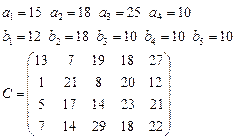 22.
22. 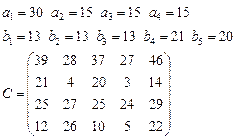
23. 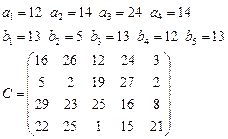 24.
24. 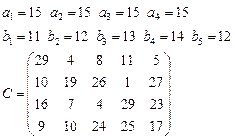
25. 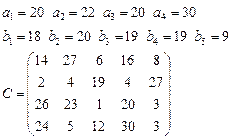 26.
26. 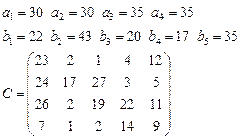
Задача 5. Найти оптимальные смешанные стратегии и цену игры, заданной матрицей 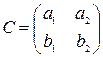 . Дать геометрическую интерпретацию решению игры. Данные приведены в следующей таблице:
. Дать геометрическую интерпретацию решению игры. Данные приведены в следующей таблице:
| № варианта | 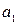 | 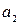 | 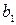 | 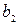 | № варианта | 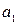 | 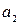 | 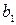 | 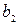 |
| -3 | |||||||||
| -4 | |||||||||
| -1 | -4 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -2 | |||||||||
| -2 | |||||||||
Задача 6. После нескольких лет эксплуатации промышленное оборудование оказывается в одном из следующих состояний:
1) оборудование может использоваться в очередном году после профилактического ремонта 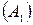 ;
;
2) для безаварийной работы следует заменить отдельные детали и узлы оборудования 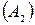 ;
;
3) оборудование требует капитального ремонта или замены 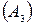 .
.
В зависимости от сложившейся ситуации руководство предприятия в состоянии принять такие решения:
1) отремонтировать оборудование силами заводских специалистов (стратегия 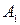 ), что потребует, в зависимости от обстановки, затрат, равных
), что потребует, в зависимости от обстановки, затрат, равных 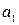 ,
, 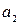 или
или 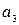 ден. ед.;
ден. ед.;
2) вызвать специальную бригаду ремонтников (стратегия 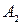 ), расходы в этом случае составят
), расходы в этом случае составят 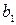 ,
, 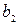 или
или 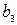 ден. ед.;
ден. ед.;
3) заменить оборудование новым, реализовав устаревшее оборудование по его остаточной стоимости (стратегия 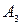 ). Совокупные затраты в этом случае будут
). Совокупные затраты в этом случае будут 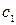 ,
, 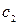 или
или 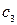 ден. ед.
ден. ед.
Требуется:
1) придать описанной ситуации игровую схему, установить характер игры, указав возможные чистые стратегии;
2) составить платежную матрицу;
3) используя различные критерии оптимальности, выяснить, какое решение целесообразно рекомендовать руководству предприятия, чтобы минимизировать потери, предположив, что вероятности указанных выше состояний равны соответственно 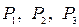 , коэффициент
, коэффициент 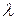 задается. Данные приведены в следующей таблице:
задается. Данные приведены в следующей таблице:
| № варианта | 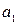 | 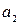 | 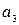 | 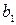 | 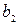 | 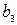 | 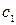 | 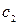 | 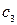 | 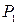 | 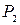 | 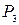 | 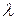 | ||||
| 0,30 | 0,50 | 0,20 | 0,7 | ||||||||||||||
| 0,40 | 0,45 | 0,15 | 0,9 | ||||||||||||||
| 0,15 | 0,60 | 0,25 | 0,5 | ||||||||||||||
| 0,15 | 0,55 | 0,30 | 0,8 | ||||||||||||||
| 0,20 | 0,65 | 0,15 | 0,6 | ||||||||||||||
| 0,35 | 0,45 | 0,20 | 0,8 | ||||||||||||||
| 0,35 | 0,50 | 0,85 | 0,7 | ||||||||||||||
| 0,15 | 0,65 | 0,20 | 0,9 | ||||||||||||||
| 0,35 | 0,55 | 0,10 | 0,6 | ||||||||||||||
| 0,30 | 0,45 | 0,25 | 0,7 | ||||||||||||||
| 0,3 | 0,4 | 0,3 | 0,4 | ||||||||||||||
| 0,4 | 0,5 | 0,1 | 0,6 | ||||||||||||||
| 0,6 | 0,2 | 0,2 | 0,5 | ||||||||||||||
| 0,3 | 0,3 | 0,4 | 0,6 | ||||||||||||||
| 0,2 | 0,4 | 0,4 | 0,7 | ||||||||||||||
| 0,4 | 0,3 | 0,3 | 0,4 | ||||||||||||||
| 0,5 | 0,3 | 0,2 | 0,6 | ||||||||||||||
| 0,3 | 0,5 | 0,2 | 0,5 | ||||||||||||||
| 0,4 | 0,1 | 0,5 | 0,4 | ||||||||||||||
| 0,3 | 0,4 | 0,3 | 0,6 | ||||||||||||||
| 0,2 | 0,4 | 0,4 | 0,7 | ||||||||||||||
| 0,3 | 0,6 | 0,1 | 0,5 | ||||||||||||||
| 0,4 | 0,2 | 0,4 | 0,4 | ||||||||||||||
| 0,5 | 0,3 | 0,2 | 0,6 | ||||||||||||||
| 0,2 | 0,5 | 0,3 | 0,5 | ||||||||||||||
| 0,4 | 0,3 | 0,3 | 0,7 | ||||||||||||||
| 0,3 | 0,2 | 0,5 | 0,6 | ||||||||||||||
| 0,4 | 0,2 | 0,4 | 0,4 | ||||||||||||||
| 0,5 | 0,3 | 0,2 | 0,5 | ||||||||||||||
| 0,6 | 0,2 | 0,2 | 0,7 | ||||||||||||||
 2015-10-16
2015-10-16 833
833






