Гипербола

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2а.

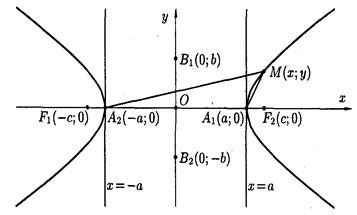Точки F₁ и F₂ имеют координаты F₁ (c, 0) и F₂(-c, 0).

Пусть точка М (х,у) – некоторая точка плоскости. Обозначим через r₁ и r₂ расстояния от точки М до точек F₁ и F₂ соответственно. Согласно определению гиперболы равенство:

|r₁-r₂|=2a

является необходимым и достаточным условием расположения точки М (х,у) на данной гиперболе.

Уравнение гиперболы в данной системе координат примет вид:

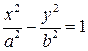- каноническое уравнение гиперболы,

где b²=c²-a².

Если а=b, то гипербола называется равносторонней.

Свойства гиперболы.

1) Гипербола симметрична относительно осей Ох и Оу и точки О (0;0) – центра гиперболы.

2) Гипербола состоит из двух частей, называемых ветвями гиперболы.

Точки пересечения гиперболы с осью Ох А₁ (а; 0) и А₂ (- а; 0) называются вершинами гиперболы.

Отрезок А₁А₂=2а называется действительной осью гиперболы.

3) Прямые 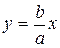и 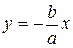называются асимптотами гиперболы ( ветви гиперболы неограниченно приближаются к этим прямым).

Отношение расстояния между фокусами к длине действительной оси эллипса называется эксцентриситетом гиперболы:

е=с/а.

Учитывая, что b²=с²-а², получим:

.

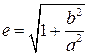Из этой формулы видно, что эксцентриситет гиперболы больше единицы.

Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины угла между ее асимптотами, т.к. отношение 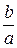есть тангенс половины угла между асимптотами гиперболы.