I. Найти неопределенные интегралы.
1. а) 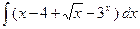 , б)
, б) 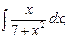
в) 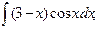 г)
г) 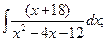
2. а) 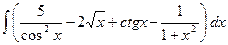 , б)
, б) 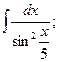
в) 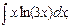 г)
г) 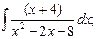
3. а) 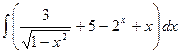 , б)
, б) 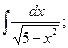
в) 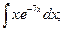 г)
г) 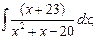
4. а) 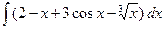 , б)
, б) 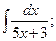
в) 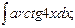 г)
г) 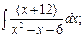
5. а) 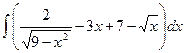 , б)
, б) 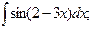
в) 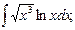 г)
г) 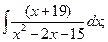
6. а) 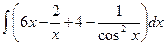 , б)
, б) 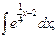
в) 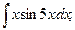 г)
г) 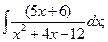
7. а) 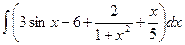 , б)
, б) 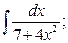
в) 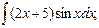 г)
г) 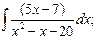
8. а) 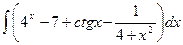 , б)
, б) 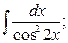
в) 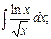 г)
г) 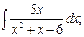
9. а) 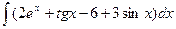 , б)
, б) 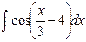
в) 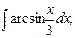 г)
г) 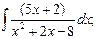
10. а) 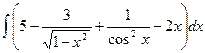 , б)
, б) 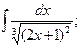
в) 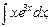 г)
г) 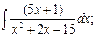
11. а) 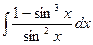 , б)
, б) 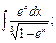
в) 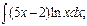 г)
г) 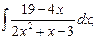
12. а) 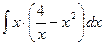 , б)
, б) 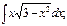
в) 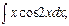 г)
г) 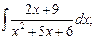
13. а) 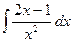 б)
б) 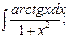
в) 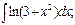 г)
г) 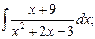
14. а) 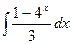 , б)
, б) 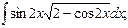
в) 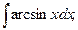 г)
г) 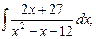
15. а) 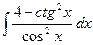 , б)
, б) 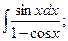
в) 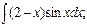 г)
г) 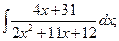
16. а) 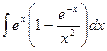 , б)
, б) 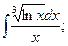
в) 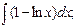 г)
г) 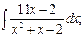
17. а)  , б)
, б) 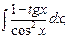
в) 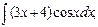 г)
г) 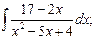
18. а) 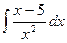 , б)
, б) 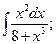
в) 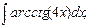 г)
г) 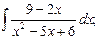
19. а) 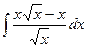 , б)
, б) 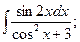
в) 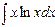 , г)
, г) 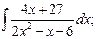
20. а) 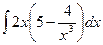 , б)
, б) 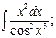
в) 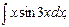 г)
г) 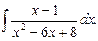
II. а) Вычислить определенный интеграл.
1. 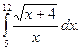 2. 2. 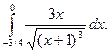 3. 3. 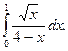 4. 4. 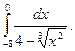 5. 5. 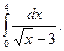 6. 6. 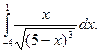 7. 7. 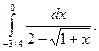 8. 8. 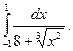 9. 9. 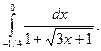 10. 10. 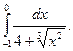 | 11. 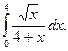 12. 12. 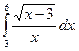 13. 13. 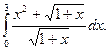 14. 14. 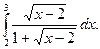 15. 15. 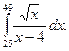 16. 16. 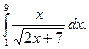 17. 17. 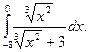 18. 18. 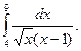 19. 19. 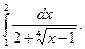 20. 20. 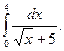 |
б) Вычислить несобственный интеграл или установить его расходимость.
1. 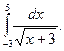 2. 2. 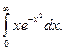 3. 3. 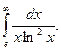 4. 4. 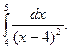 5. 5. 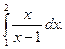 6. 6. 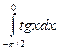 7. 7. 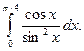 8. 8. 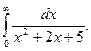 9. 9. 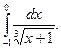 10. 10. 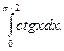 | 11. 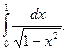 12. 12. 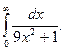 13. 13. 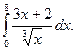 14. 14. 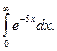 15. 15. 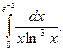 16. 16. 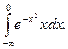 17. 17. 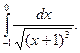 18. 18. 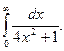 19. 19. 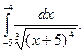 20. 20. 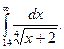 |
III. Вычислить площадь фигуры, ограниченной линиями:
| 11. 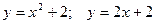 ; 12. ; 12. 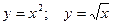 ; 13. ; 13. 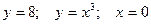 ; 14. ; 14. 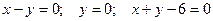 ; 15. ; 15. 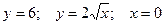 ; 16. ; 16. 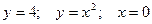 ; (I четверть); 17. ; (I четверть); 17. 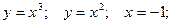 18. 18. 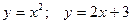 ; 19. ; 19. 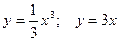 ; 20. ; 20. 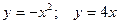 . . |
IV. Решить задачи:
1. Какую работу совершает сила в 10 Н при растяжении пружины на 2 см?
2. Какую работу надо затратить, чтобы растянуть пружину на 0,05 м, если сила в 1 Н растягивает ее на 0,01 м?
3. Для сжатия пружины на 3 см необходимо совершить работу в 16 Дж. На какую длину можно сжать пружину, совершив работу в 144 Дж?
4. Вычислите силу давления воды на одну из стенок аквариума, имеющего длину 30 см и высоту 20 см.
5. Вычислите силу давления воды на погруженную в нее вертикальную пластину, имеющую форму треугольника с основанием 6 м и высотой 2 м, предполагая, что вершина этого треугольника лежит на свободной поверхности воды, а основание параллельно ей.
6. Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы растянуть пружину на 6 см?
7. Найти давление воды, находящейся в цилиндрическом баке высотой 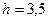 м и радиусом
м и радиусом 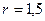 м, на его стенки.
м, на его стенки.
8. Скорость точки, движущейся прямолинейно, задана уравнением 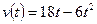 . Вычислите её путь от начала движения до остановки.
. Вычислите её путь от начала движения до остановки.
9. Скорость точки, движущейся прямолинейно, задана уравнением 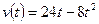 . Вычислите её путь за 3 секунды.
. Вычислите её путь за 3 секунды.
10. Скорость точки, движущейся прямолинейно, задана уравнением 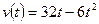 . Вычислите её путь за четвертую секунду.
. Вычислите её путь за четвертую секунду.
Найти объем тела, полученного вращением фигур, ограниченных линиями вокруг указанной оси:
11. 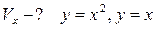 ;
;
12. 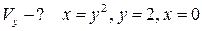 ;
;
13. 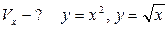 ;
;
14. 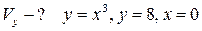 ;
;
15. 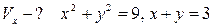 ;
;
16. 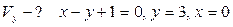 ;
;
17. 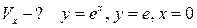 ;
;
18. 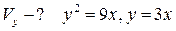 ;
;
19. 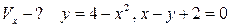 ;
;
20. 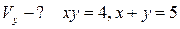 .
.
 2015-10-16
2015-10-16 1381
1381

 ;
;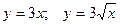 ;
;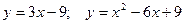 ;
;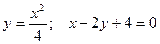 ;
;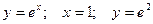 ;
;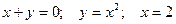 ;
;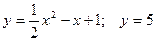 ;
;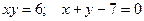 ;
;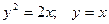 ;
;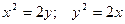 ;
;