VI. Вычислить криволинейный интеграл

1. 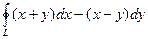, где L – окружность 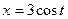, , 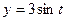пробегаемая в положительном направлении.

2. 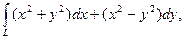где L – ломанная 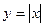от точки А(-1;1) до точки B(2,2).

3. 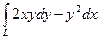, где L – дуга параболы 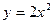от точки А(1;2) до точки B(2;8).

4. 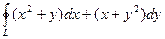, где L – контур треугольника с вершинами (указанными в порядке обхода) в точках А(1;2), В(1;5), С(0;5).

5. 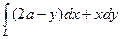, где L – дуга первой арки циклоиды , .

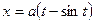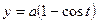6. 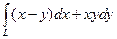, где L – отрезок, соединяющий точки А(1;1) и В(3;5).

7. 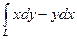, где L – четверть астроиды , ().

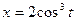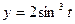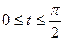8. 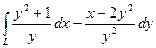, где L – отрезок, соединяющий точки А(1;2) и В(2;4).

9. 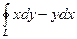, где L – контур треугольника с вершинами А(-1;0), В(1;0), С(0;1), пробегаемый в положительном направлении.

10. 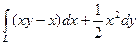, где L – дуга параболы 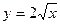от точки А(0;0) до точки В(1;2).

11. 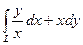, где L – дуга линии 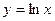от точки А(1;0) до точки В(e;1).

12. 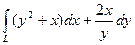, где L – дуга экспоненты 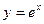от точки А(0;1) до точки В(1;e)

13. 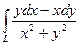, где L – верхняя полуокружность 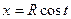, , 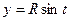пробегаемая в положительном направлении.

14. 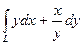, где L – дуга экспоненты 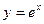от точки А(0;1) до точки В(-1;e).

15. 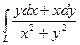, где L – отрезок прямой от точки А(1;2) до точки В(3;6).

16. 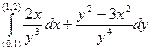, вдоль ломанной АВС, где А(0;1), В(1;1), С(1;2).

17. 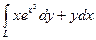, где L – дуга параболы 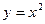от точки А(1;1) до точки В(2;4).

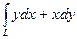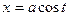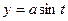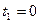18. , где L – дуга окружности , от до .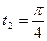

19. 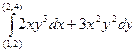вдоль отрезка, соединяющего указанные точки.

20. 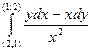вдоль ломаной АВС, где А(2;1), В(2;2), С(1;2).