1. Провести многократное измерение величины X несколько раз и результаты занести в таблицу 1 (Хi, где i =1, 2,.n, где n- число измерений).
2. Найти средне арифметическое значение <Х> = (Х1+ Х2+..+ Хn)/n и записать в таблицу 1.
3. Найти модули разности |Хi - <Х>| = DХi для каждого измерения и занести их в таблицу 1.
4. Вычислить квадраты абсолютных погрешностей (DХi)2, результаты записать в таблицу 1.
5. Вычислить сумму квадратов Sх = (DХ1)2 +..+ (DХn)2,а затем и средне квадратичную погрешность результатов измерений: 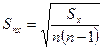 .
.
6. По таблице 2 с учётом заданной преподавателем надежности α и числа измерений n определить коэффициент Стьюдента tna..
7. Вычислить абсолютную погрешность результата измерений: DХр = tna×Snх.
8. Полная абсолютная погрешность результата измерений
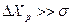 , то
, то 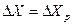 ;
;
2) если 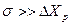 , то
, то 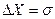 ;
;
3) если 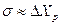 , то
, то 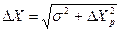 .
.
9. Вычислить относительную погрешность измерений 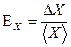 , все результаты занести в таблицу 1..
, все результаты занести в таблицу 1..
10. Окончательный результат округлить и записать в форме: Х = (<Х> ± DХ) ед. измерения.
Пример. Ответ: плотность цилиндра r = (7,82 ± 0,05)×103 кг/м3.
- Погрешности косвенных измерений определяются по формуле:
Если 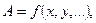 то
то 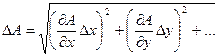 или в частных случаях:
или в частных случаях:
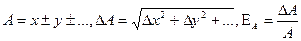
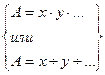
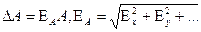
Таблица 1 Таблица 2. Коэффициенты Стьюдента 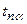
  n
n
| 0.5 | 0.7 | 0.9 | 0.95 | 0.99 |
| 1,0 | 2,0 | 6,3 | 12,7 | 63,7 | |
| 0,82 | 1,3 | 2,9 | 4,3 | 9,9 | |
| 0,77 | 1,3 | 2,4 | 3,2 | 5,8 | |
| 0,74 | 1,2 | 2,1 | 2,8 | 4,6 | |
| 0,73 | 1,2 | 2,0 | 2,6 | 4,0 | |
| 0,70 | 1,1 | 1,8 | 2,3 | 3,3 |
| № | Хi | DХi | (DХi)2 | Данные и результат |
| Х1 | DХ1 | (DХ1)2 | 
| |
| Х2 | DХ2 | (DХ2)2 | 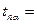
| |
| Х3 | DХ3 | (DХ3)2 | 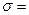
| |
| … | … | …. | ….. | 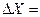
|
| n | Xn | DХn | (DХn)2 | |

| <Х> | DХр | Snx | 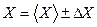
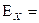
|
 2015-10-16
2015-10-16 392
392







