Определение объёма прямоугольной пластинки с помощью штангенциркуля

1 2 3 4

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ

АКАДЕМИЯ»

Кафедра физики

Лаборатория механики и молекулярной физики №1 (213а)

ЛАБОРАТОРНАЯ РАБОТА №1

ИЗМЕРЕНИЕ РАЗМЕРОВ И ОПРЕДЕЛЕНИЕ ОБЪЁМОВ ТЕЛ ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ

Cоставил: доцент кафедры физики

Идиатулин В.С.

Ижевск 2013

ЛАБОРАТОРНАЯ РАБОТА №1

ИЗМЕРЕНИЕ РАЗМЕРОВ И ОПРЕДЕЛЕНИЕ ОБЪЁМОВ ТЕЛ ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ

Цель работы: приобретение навыков пользования штангенциркулем и микрометром. Измерение размеров заданных тел.

Приборы и принадлежности: 1) штангенциркуль, 2) микрометр, 3) измеряемые тела.

Для определения объёма тела правильной геометрической формы бывает достаточно измерить его линейные размеры. Из измерительных инструментов в этом случае обычно используются штангенциркуль и микрометр.

ЗАДАНИЕ 1.

ОПРЕДЕЛЕНИЕ ОБЪЁМА ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ С ПОМОЩЬЮ ШТАНГЕНЦИРКУЛЯ

Штангенциркуль представляет собой линейку, на которой нанесена шкала, разделённая на миллиметры. Эта шкала называется основной. Линейка снабжена двумя ножками, из которых одна подвижная. На подвижной ножке штангенциркуля имеется вторая шкала – нониус. Нониус представляет собой короткую линейку, скользящую вдоль основной шкалы вместе с ножкой. В некоторых штангенциркулях нониус разделён на 10 равных делений, а вся его длина 19 мм, т.е. каждое деление нониуса короче 2-х мм основной шкалы на 0,1 мм. Когда ножки штангенциркуля сдвинуты до соприкосновения, то ноль нониуса совпадает с нулём основной шкалы, а деление 10 нониуса совпадает с делением 19 основной шкалы (рис. 1). Такой прибор даёт возможность измерять размеры тел с точностью до 0,1 мм.

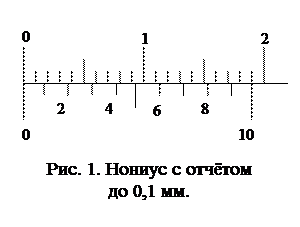Измеряемое тело помещают между ножками штангенциркуля и сдвигают подвижную ножку до полного соприкосновения с телом. Затем производят отсчёт. Сначала нужно отсчитать, сколько целых миллиметров укладывается до нулевого деления нониуса по основной шкале. Если бы ноль нониуса точно совпадал с каким-нибудь делением основной шкалы, то мы бы получили размеры тела в целых миллиметрах. Но обычно ноль нониуса не совпадает с делением основной шкалы и смещается от него на некоторую долю.

Рассмотрим рис. 2. Прежде всего определим, сколько целых миллиметров укладывается до нулевого деления нониуса. В данном случае до нулевого деления укладывается 2 мм. Но размеры тела больше, чем 2 мм, т.к. нулевое деление нониуса лежит между вторым и третьим делением основной шкалы. Нужно определить, какое деление нониуса точно совпадает с делением основной шкалы. На рис. 2 с делением основной шкалы совпадает восьмое деление нониуса, что соответствует 0,8 мм. Таким способом могут быть измерены все наружные размеры тела. Для определения внутренних размеров, например, диаметр отверстий и т.п. пользуются ножками, находящимися в верхней части штангенциркуля.

При измерении внутренних размеров отверстия эти ножки спускают в отверстие и там раздвигают до соприкосновения со стенками, после чего производят отсчёт по основной шкале и нониусу таким же путём, как это было описано выше.

В других штангенциркулях нониус разделён на 20 делений и имеет длину 39 мм, т.е. каждое деление нониуса короче 2-х мм основной шкалы на 0,05 мм. Такой прибор даёт возможность измерять размеры тел с точностью до 0,05 мм (рис. 3).

При пользовании этим штангенциркулем также определяют сначала, сколько целых миллиметров укладывается до нулевого деления нониуса, а затем определяют, какое деление нониуса точно совпадает с делением шкалы.

Пример: ноль нониуса расположен между делением 11 и 12 основной шкалы. Совпадает с делением основной шкалы пятое деление нониуса. Размер тела 11 + 5^.0,5 = 11,25 мм.

На практике для отсчёта сотых долей совпадающее деление нониуса умножать не приходится. Как видно из рис. 4 против пятого деления нанесено число 25, против десятого деления – число 50 и т.д. Числа, отсчитанные на шкале нониуса, и соответствуют сотым долям.

Объём параллелепипеда равен произведению его длины l на ширину a и высоту h. Измерение каждой из этих величин производится многократно и определяется среднее арифметическое < l>, <a>, <h>. Тогда объём будет равен:

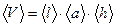. (1)