1. Произвести измерение длины l, ширины a и высоты h прямоугольной пластинки (параллелепипеда). Измерение каждой величины провести несколько раз, наиболее важно определить максимальное и минимальное значение lmax и lmin, amax и amin, hmax и hmin. Среднее значение находится как полусумма измеренных максимального и минимального значений. Например, 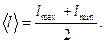 Результаты всех измерений занести в таблицу 1 с указанием единиц измерения.
Результаты всех измерений занести в таблицу 1 с указанием единиц измерения.
Таблица 1 Измерения размеров пластинки
| lmax = | amax = | hmax = |
| lmin = | amin = | hmin = |
| <l> = | < a > = | <h> = |
| ∆lp = | ∆ap = | ∆hp = |
| ∆l = | ∆a = | ∆h = |
| εl = | εa = | εh = |
2. Абсолютную погрешность измерения ∆lp длины оценить по любой из формул: 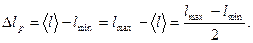
Найденную абсолютную погрешность нужно обязательно сравнить с погрешностью измерительного прибора δ, в данном случае штангенциркуля, она указана на его подвижной шкале (нониусе). В качестве окончательного результата следует взять наибольшую из величин δ и ∆lp, т.е.
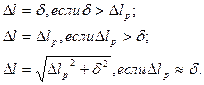
Относительная погрешность длины: 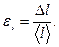
Аналогичным образом находятся погрешности ширины и высоты.
Все результаты занести в таблицу 1.
3. Вычислить объём пластинки по формуле: 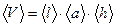 . Записать результат в таблицу 2. Погрешность объёма можно оценить следующим способом: вычислить наибольшее значение объёма по данным измерениям, т.е.
. Записать результат в таблицу 2. Погрешность объёма можно оценить следующим способом: вычислить наибольшее значение объёма по данным измерениям, т.е.
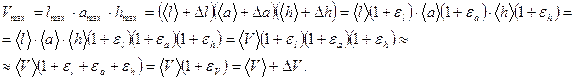
Аналогичным образом эту оценку можно было бы сделать через минимальное значение: 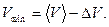
Результат принято записывать в следующем виде:
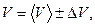 (2)
(2)
причём погрешность находится либо как 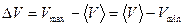 , либо находится по правилу сложения максимальной относительной погрешности:
, либо находится по правилу сложения максимальной относительной погрешности: 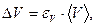 где
где 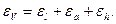 (3)
(3)
Таблица 2 Вычисление объёма пластинки
Объём 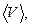 мм3 мм3
| Средняя абсолютная погрешность
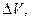 мм3 мм3
| Средняя относительная погрешность
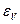
| Окончательный результат
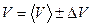
|
 2015-10-16
2015-10-16 350
350








