МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ
АКАДЕМИЯ»
Кафедра физики
Лаборатория механики и молекулярной физики №1(213а)
ЛАБОРАТОРНАЯ РАБОТА №8
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАТУХАНИЯ
Отредактировал: Кораблев Г.А.
Ижевск 2013
ЛАБОРАТОРНАЯ РАБОТА №8
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАТУХАНИЯ
Цель работы: ознакомление с характером собственных колебаний и вычисление коэффициента затухания.
Приборы и принадлежности: 1) маятник со шкалой отсчёта, 2) электросекундомер.
Колебательным называется движение, при котором материальная точка или тело многократно отклоняясь от своего положения равновесия, вновь возвращается к нему. Время одного полного колебания называется периодом. Наибольшее отклонение маятника от положения равновесия называется амплитудой колебания.
На практике всякое колебание, если оно не поддерживается извне, затухает: амплитуда колебаний с течением времени уменьшается, так как на движущееся тело действует сила трения окружающей среды.
Результирующая сила F, действующая на тело, равна сумме квазиупругой силы 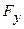 и силы трения
и силы трения 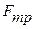 . При малых скоростях движения сила трения пропорциональна скорости и направлена в противоположную сторону, т. е.
. При малых скоростях движения сила трения пропорциональна скорости и направлена в противоположную сторону, т. е. 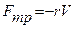 , где r- коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
, где r- коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
По второму закону Ньютона F = ma, или 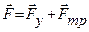 (1)
(1)
Если учесть, что 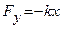 ,
, 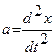 и
и 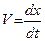 , то формула (1) примет вид
, то формула (1) примет вид 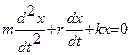 (2)
(2)
или 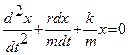 (3)
(3)
Это и есть дифференциальное уравнение затухающих колебаний. Оно имеет два решения 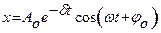 или
или 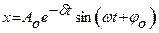 , где
, где 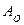 и
и 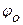 - соответственно начальные амплитуды и фаза, х – смещение в данный момент времени,
- соответственно начальные амплитуды и фаза, х – смещение в данный момент времени, 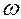 – циклическая частота, равная
– циклическая частота, равная 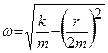 ,
, 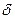 – коэффициент затухания, равный
– коэффициент затухания, равный 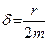 , e – основание натуральных логарифмов. Величина
, e – основание натуральных логарифмов. Величина 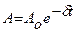 – амплитуда колебаний, убывает с течением времени. Быстроту уменьшения ее характеризует коэффициент
– амплитуда колебаний, убывает с течением времени. Быстроту уменьшения ее характеризует коэффициент 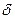 , он обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.
, он обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.
В данной работе нужно определить коэффициент затухания колебаний для маятника.
Чтобы получить более удобное выражение для определения 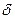 , возьмем отношение двух амплитуд, разделённых отрезком времени в один период
, возьмем отношение двух амплитуд, разделённых отрезком времени в один период 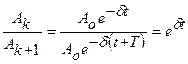 , т. е. амплитуда за каждый период убывает в одно и то же число раз.
, т. е. амплитуда за каждый период убывает в одно и то же число раз.
Натуральный логарифм этого отношения
|

 ln
ln 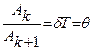 (4)
(4)
носит название логарифмического декремента затухания.
Таким образом, чтобы определить коэффициент затухания 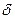 , нужно определить логарифмический декремент θ и период Т.
, нужно определить логарифмический декремент θ и период Т.
|

|

|
|
 2015-10-16
2015-10-16 576
576







