2015-10-16
969
1. Определить по миллиметровой линейке положение равновесия маятника.
2. Отклонив маятник от положения равновесия вправо на некоторый угол (не более 5-60), измерить начальную амплитуду.
3. Измерить не менее 5 амплитуд вправо, разделённых промежутком времени в один период.
4. Отклонив маятник на тот же угол и в ту же сторону, как в первом случае, измерить 5 левых амплитуд. Все данные занести в таблицу 1.
5. По измеренным данным найти отношение амплитуд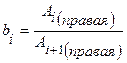 
и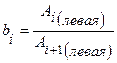 
, разделённых интервалом в один период, и занести их в таблицу 1.
6. По стандартной методике, приведённой в приложении, найти абсолютную и относительную погрешности для b. Коэффициент надёжности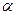 
задаёт преподаватель. Результаты занести в таблицу 1.
7. Вычислить логарифмический декремент затухания по формуле: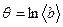 
,
а также его погрешности: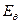 
= Е b, 
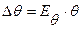. Результаты занести в таблицу 2.
8. Округлив полученные результаты, записать ответ по форме:
Ответ: логарифмический декремент затухания равен:
θ = (<θ>± Dθ)
Результаты занести в таблицу 2.
Пример. Ответ: момент инерции диска равен:
I = (0,10 ± 0,01) кг×м2. 
Таблица 1 Измерение амплитуд свободных колебаний
| № изм. | Амплитуды | bi | Δ bi | (Δ bi)2 | Данные и результат | |
| Правые | ||||||
| < b >= | ||||||
| n(n-1)= | ||||||
Sn b =  = | ||||||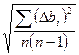
| = | ||||||
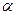| tnα = | ||||||
| Левые | Δ bp= Snb. tnα = | |||||
| Δ b = | ||||||
Е b =  = | ||||||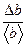
| Δ A = | ||||||
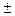b= < b>  Δ b = | ||||||
Таблица 2 Определение логарифмического декремента
| Логарифмический декремент θ | 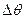 | 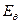| θ = (<θ>± Dθ) ед. измерения |
