· Степенью числа а называется произведение п множителей, каждый из которых равен а, т.е. 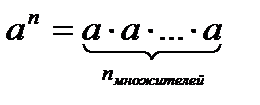 , где а – основание, п – показатель степени.
, где а – основание, п – показатель степени.
Свойства степени:
1. ап · ак = ап+к
2. ап: ак = ап-к
3. (ап)к=апк
4. ап·вп=(ав)п
5. 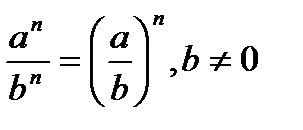
9. Если а 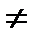 0, то а0=1, (2)0=1, 00 не имеет смысла.
0, то а0=1, (2)0=1, 00 не имеет смысла.
10. Если а 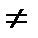 0, то
0, то 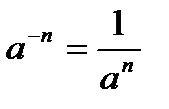 и
и 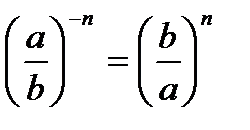
Корень n –ой степени и его свойства
· Корнем n –ной степени из числа x называется такое число y, n –ая степень которого равна х.
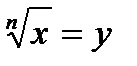 ,
, 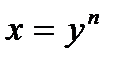
· Степенью с дробно – рациональным показателем называется выражение:
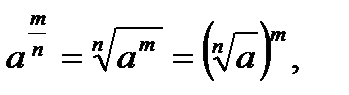 где
где 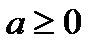 и
и 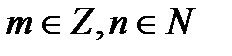
Свойства:
1) 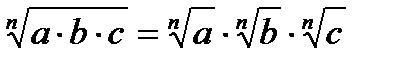 4)
4) 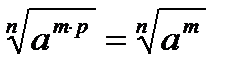
2) 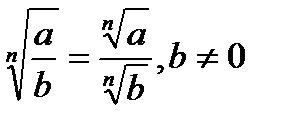 5)
5) 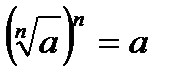
3) 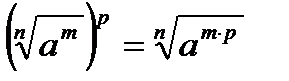 6)
6) 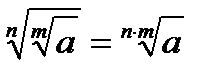
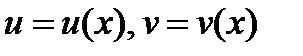
1) 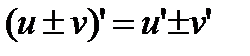 3)
3) 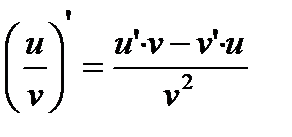
2) 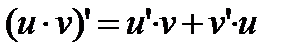 4)
4) 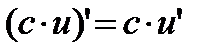
Формулы дифференцирования
1) 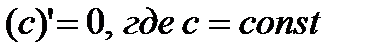 2) 2) 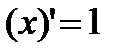 3) 3) 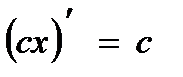 4) 4) 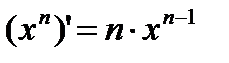 5) 5) 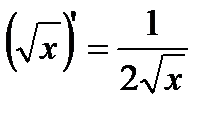 6) 6) 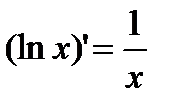 7) 7) 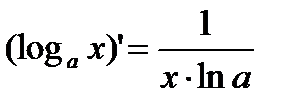 8) 8) 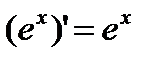 9) 9) 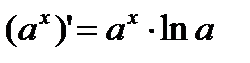 | 10) 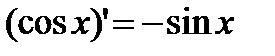 11) 11) 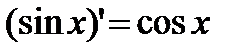 12) 12) 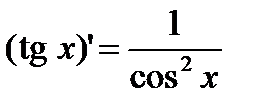 13) 13) 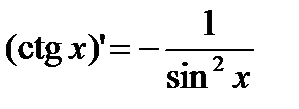 14) 14) 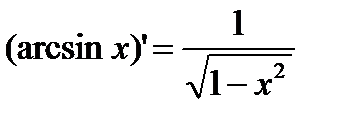 15) 15) 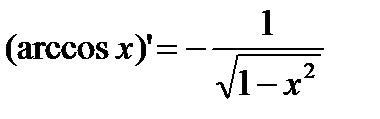 16) 16) 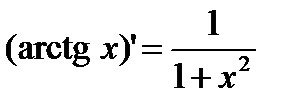 17) 17) 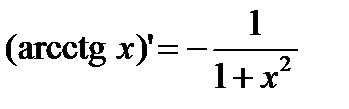 |
Основные формулы интегрирования:
1. 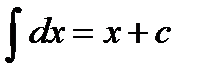 | 8. 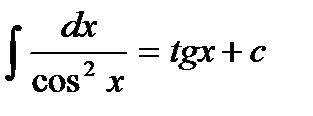 |
2. 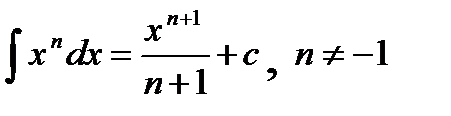 | 9. 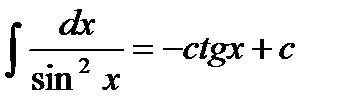 |
3. 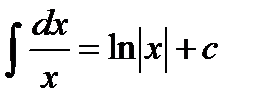 | 10. 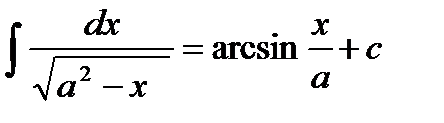 |
4. 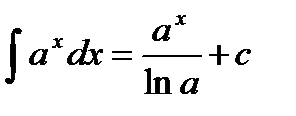 | 11. 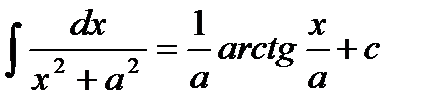 |
5. 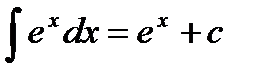 | 12. 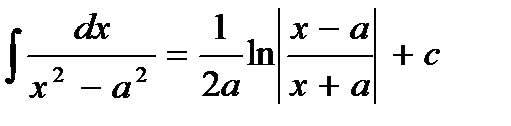 |
6. 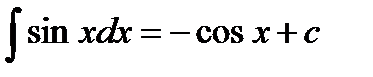 | |
7. 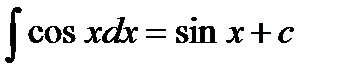 |
Приложение 2
 2015-10-16
2015-10-16 760
760








