Доказанные в предыдущей лекции теоремы имеют важные приложения, в частности, теорема Коши приводит к новому для, нас методу вычисления пределов.
Задача 1 (правило Лопиталя)
Пусть f(x) и g (x) дифференцируемы в точке x 0, причём
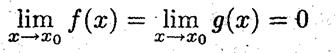
Показать, что
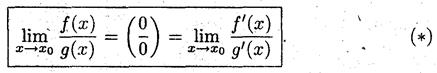
Ø Доопределим заданные функции в точке x 0, а именно, f(xo) = g(xo) =0. Тогда согласно теореме Коши найдётся такая точка ξ 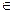 (x,x0), в которой выполняется соотношение
(x,x0), в которой выполняется соотношение
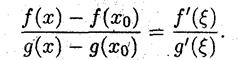
Вычисление предела от этого соотношения
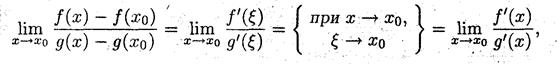
приводит к правилу Лопиталя (*). >
* Предел частного дифференцируемых функций, в случае неопределённости вида (0/0), равен пределу частного производных функций, если этот предел существует.
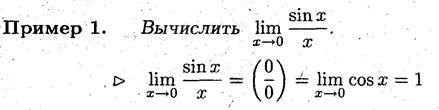

Замечание 3. Правило Лопиталя можно применять для вычисления предела в бесконечно удаленной точке.

Замечание 4. Правило Лопиталя после простого преобразования можно применять для раскрытия неопределённостей вида (0•∞).
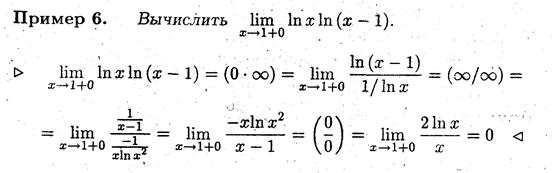
Задача 3
Свести неопределённость вида (∞ - ∞) к неопределённости вида (0/0).
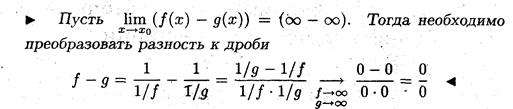
Замечание 5. Правило Лопиталя можно применять для раскрытия неопреде -лённостей вида (∞ - ∞), поскольку она сводится к неопределённости вида (0/0).
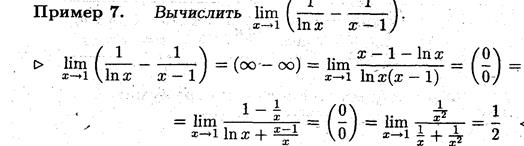
Задача 4
Свести неопределённости вида (1∞), (0∞), (∞ 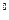 ) к неопределённости вида (0 • ∞)
) к неопределённости вида (0 • ∞)
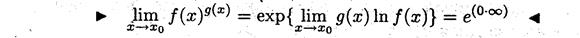
Замечание 6. Правило Лопиталя после логарифмирования можно применять для раскрытия неопределённостей вида
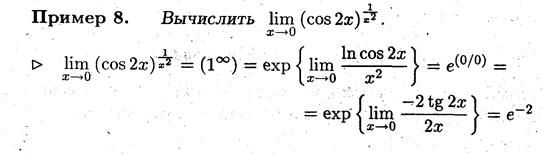
 2015-07-14
2015-07-14 2337
2337