Коллинеарные векторы

Два ненулевых 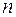-мерных вектора 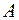и 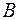называются коллинеарными, если угол между ними равен 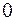или .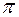

Если 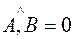, то коллинеарные векторы называются сонаправленными или одинаково направленными .

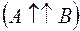Если 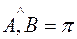, то коллинеарные векторы называются противоположно направленными .

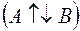Если условие коллинеарности между векторам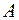и и 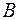не выполняется (т.е. 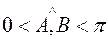), то такие вектора называются неколлинеарными.

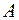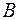Теорема. Ненулевые векторы и коллинеарны тогда и только тогда, когда найдется такое ненулевое числ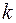о , что .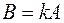

Доказательство:

Необходимость:

1. .

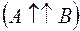
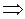
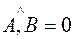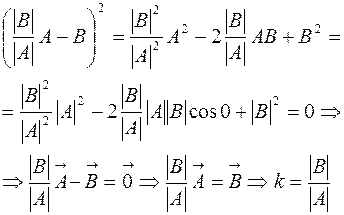
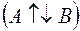
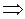
2. 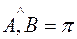. Для этого случая аналогично доказывается, что 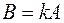, при .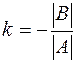

Достаточность:

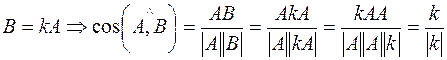
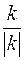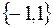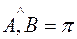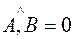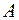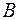Число имеет только два значения: . Это означает, что или , соответственно. Таким образом, вектора и коллинеарны.