Английский ученый Роберт Гук в середине 17 века экспериментально установил прямую пропорциональную зависимость между силой F, приложенной к стержню, и абсолютным удлинением стержня Δ l (рис. 3).
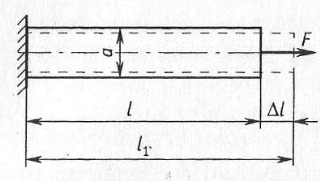
Рис. 3. Растяжение стержня
Позднее французский ученый Коши ввел понятие «напряжение» (σ), а Юнг – понятие «модуль упругости» (Е), и закон Гука принял следующий вид:
σ = Е·ε, (1)
где ε = Δl / l – относительное удлинение стержня (деформация);
Е – модуль упругости, Па, МПа. Характеризует способность материала сопротивляться упругому деформированию (для стали Ест = 2·1011 Па).
По закону Гука продольная деформация прямо пропорциональна напряжению.
Интересно отметить, что усовершенствование формы записи закона Гука заняло приблизительно 150 лет.
При растяжении стержня его поперечные размеры уменьшаются. По аналогии с продольной деформацией можно записать (см. рис. 3):
εп = Δа / а,
где εп – поперечная деформация
Поперечная и продольная деформации связаны между собой:
εп = – µ ε, (2)
где µ – коэффициент поперечной деформации (коэффициент Пуассона);
µ = 0…0,5 (0 имеет пробка, 0,5 – резина; у стали µ = 0,3).
Из закона Гука следует, что на участке длиной l с постоянной площадью сечения и постоянной продольной силой удлинение стержня равно:
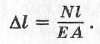 (3)
(3)
ЕА – жесткость сечения при растяжении.
Если площадь сечения и продольная сила по длине стержня меняются, нужно пользоваться формулой
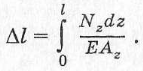
 2015-10-16
2015-10-16 1557
1557








