I. Перевод чисел в десятичную систему счисления
Для того чтобы перевести число из любой системы счисления в десятичную, поступают следующим образом:
1) нумеруют разряды числа справа налево, начиная с нулевого;
2) вычисляют сумму произведений степеней основания системы счисления и цифр числа. Такая запись называется расширенной записью числа.
Запись чисел в каждой из систем счисления с основанием p означает сокращенную запись выражения
Общая форма представления расширенной записи числа:
an-1 pn-1 + an-2 pn-2+... + a1 p1 + a0 p0 + a-1 p-1 +... + a-m p-m, (1.3.1)
где ai - цифры системы счисления; n и m - число целых и дробных разрядов, соответственно.
Пример
Перевести двоичное число 10111012 в десятичную систему счисления.
Решение.
Пронумеруем разряды числа справа налево, начиная с нулевого. Вычислим сумму произведений степеней основания системы счисления и цифр числа. Получим:
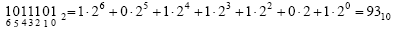
Ответ: 10111012 = 9310.
Пример
| -1 | =1*23+1*22+0*21+1*20+1*2-1 | |||||
| , |
Ответ:10111012=13,210
Таблица степеней числа 2 в 10 -ичной и 8 -ичной системах.
| Степени двойки | Десятичное представление | Восьмеричное представление |
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 | ||
| 210 | ||
| 211 | ||
| 212 | ||
| Запись степеней двойки с исполь-зованием десятич-ной системы | Запись чисел в десятичной системе, то есть с помощью цифр этой системы: 0,1,2,3,4,5,6,7,8,9 | Запись чисел в восьмерич-ной системе, с помощью цифр этой системы: 0,1,2,3,4,5,6,7[M1] |
 2015-10-13
2015-10-13 439
439








