s=f(t) – естественный способ задания движения, прямолинейное движение: х=f(t).
Координатный способ: x=f1(t), y=f2(t), z=f3(t). Уравнение траектории: f(x,y,z)=0.
Векторный способ: радиус-вектор 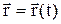 =
= 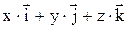 , модуль
, модуль 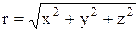 , направляющие косинусы:
, направляющие косинусы: 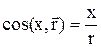 и т.д. Переход от координатного способа к естественному:
и т.д. Переход от координатного способа к естественному: 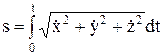 . Скорость точки. Вектор скорости:
. Скорость точки. Вектор скорости: 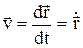 ;
; 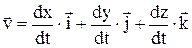 . Проекции скорости:
. Проекции скорости: 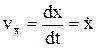 ,
, 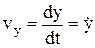 ,
, 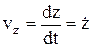 . Модуль скорости:
. Модуль скорости: 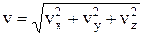 , направляющие косинусы:
, направляющие косинусы: 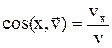 и т.д.
и т.д.
Естественный способ: 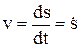 ,
, 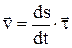 ,
, 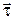 – орт касательной. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление
– орт касательной. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление 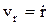 , поперечное направление
, поперечное направление 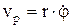 , модуль скорости
, модуль скорости 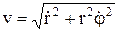 .; x=rcosj, y=rsinj. Ускорение точки.
.; x=rcosj, y=rsinj. Ускорение точки. 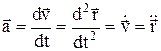 . Проекции уск.-я:
. Проекции уск.-я: 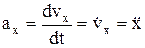 и т.д.
и т.д.
Модуль ускорения: 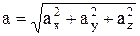 , направляющие косинусы:
, направляющие косинусы: 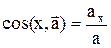 , и т.д.
, и т.д.
Проекции ускорения. на радиальное направление 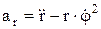 , поперечное направление
, поперечное направление 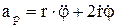 , модуль ускорения
, модуль ускорения 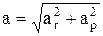 .
. 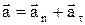 . Модуль нормального ускорения:
. Модуль нормального ускорения: 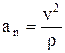 , r – радиус кривизны траектории, модуль касательного ускорения
, r – радиус кривизны траектории, модуль касательного ускорения 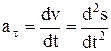 ,
, 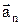 ^
^ 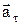 , Þ
, Þ 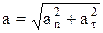 .
.
Частные случаи движения:
1. Прямолинейное движение: r= ¥, аn=0, a=at.
2. Равномерное криволинейное движение: v=const, at=0, a=an. s=s0+v×t.
3. Равномерное прямолинейное движение: а=at=an=0.
4) Равнопеременное криволинейное движение: at=const, v=v0+at×t, 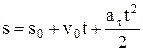 .
.
Для вращательного движения:
Угловая скорость: 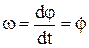 ,. Угловое ускорение тела:
,. Угловое ускорение тела: 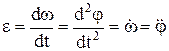 .
.
Равномерное вращение: w=const, j=wt, w=j/t, равнопеременное вращение: w=w0+et; 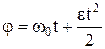 . Скорости и ускорения точек вращающегося тела:
. Скорости и ускорения точек вращающегося тела: 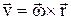 .
.
v=w×r×sin(a) = w×(ОM), (ОМ) – расстояние от точки М до оси вращения.
Формулы Эйлера: 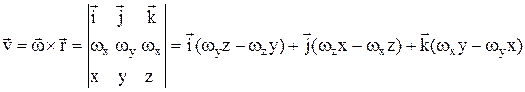 ,
,
vx=wyz – wzy; vy=wzx – wxz; vz=wxy – wyx. Если ось вращения совпадает с осью z, то vx= – wy; vy=wx. Ускорение: 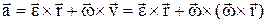 . Вращательное уск.
. Вращательное уск. 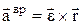 , авр=e×r×sina, центростремительное уск.
, авр=e×r×sina, центростремительное уск. 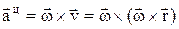 , ац=w2×R. Полное ускорение:
, ац=w2×R. Полное ускорение: 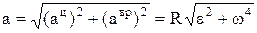 . Угол, между полным и центростремительным ускорениями:
. Угол, между полным и центростремительным ускорениями: 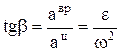 .
.
Плоское движение твердого тела, уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t).
Скорость 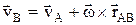 ;
; 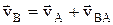 , vBA= w×BA, vAcosa = vBcosb.
, vBA= w×BA, vAcosa = vBcosb.
Мгновенный центр скоростей – Р: 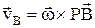 .
. 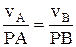 ,
, 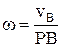 .
.
Ускорения: 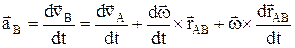 ,
,
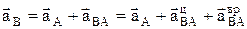 .
. 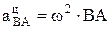 ,
, 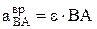 ,
, 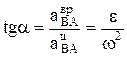 ,
, 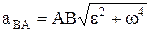 .
.
Мгновенный центр ускорений – Q; 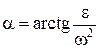 ,
, 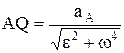 ,
, 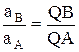 .
.
 2015-10-13
2015-10-13 642
642








