Основной закон динамики (2-ой закон (Ньютона)): 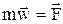 . Дифференциальные уравнения движения материальной точки:
. Дифференциальные уравнения движения материальной точки: 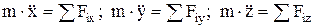 ,
,
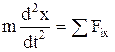 – дифференциальное уравнение прямолинейного движения точки, его общее решение:
– дифференциальное уравнение прямолинейного движения точки, его общее решение:
x=f(t,C1,C2), начальные условия: t=0, x=x0, 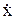 =Vx=V0.
=Vx=V0.
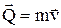 – количество движения материальной точки,
– количество движения материальной точки, 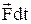 – элементарный импульс силы.
– элементарный импульс силы.
теорема об изменении количества движения материальной точки в дифференциальной форме 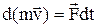 , или
, или 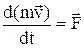 .
. 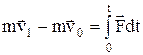
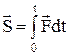 – импульс силы за [0,t]. В проекциях на оси координат:
– импульс силы за [0,t]. В проекциях на оси координат: 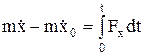 и т.д.
и т.д.
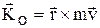 - момент количества движения материальной точки относительно центра О.
- момент количества движения материальной точки относительно центра О.
Теорема об изменении момента количества движения матер. точки. 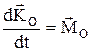 ,
, 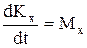 .
.
Если МО= 0, Þ 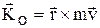 =const.
=const. 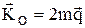 =const, где
=const, где 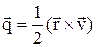 – секторная скорость. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, или dA = Fdscosa. dA=
– секторная скорость. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, или dA = Fdscosa. dA=  – скалярное произведение; dA= Fxdx+Fydy+Fzdz.
– скалярное произведение; dA= Fxdx+Fydy+Fzdz.
Работа силы на любом конечном перемещении М0М1:
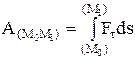 . Если F=const, то
. Если F=const, то 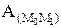 = F×s×cosa.
= F×s×cosa. 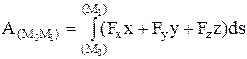 ,
, 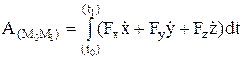 .
.
Работа силы тяжести: 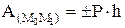 . A>0, если М0 выше М1.
. A>0, если М0 выше М1.
Работа силы упругости: 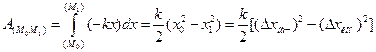 .
.
Работа силы трения: 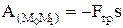 , Fтр=fN. Сила притяжения (тяготения):
, Fтр=fN. Сила притяжения (тяготения): 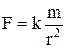 , k=gR2. Работа силы тяготения:
, k=gR2. Работа силы тяготения: 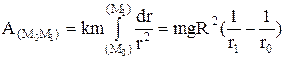 .
.
Мощность 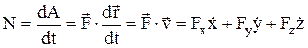 . Если N=const, то N=A/t.
. Если N=const, то N=A/t.
Теорема об изменении кинетической энергии точки. В дифференциальной форме: 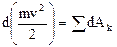 .
. 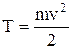 – кинетическая энергия материальной точки. В конечном виде:
– кинетическая энергия материальной точки. В конечном виде: 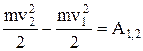 .
.
 2015-10-13
2015-10-13 575
575








