Парные (линейные) коэффициенты корреляции

Корреляционный анализ начинается с расчетапарных (линейных) коэффициентов корреляции.

Парный коэффициент корреляции представляет собой меру линейной зависимости между двумя переменными на фоне действия остальных переменных, входящих в модель.

В зависимости от того, какой порядок вычислений более удобен исследователю, расчет данного коэффициента проводят по одной из следующих формул:

1)

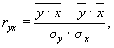
где 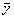¾среднее арифметическое значение у;

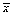¾среднее арифметическое значение х;

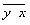¾среднее арифметическое значение из произведений у и х;

s _у ¾ среднеквадратическое отклонение признака у;

s _х ¾ среднеквадратическое отклонение признака х.

2)

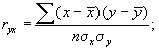
3)

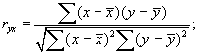
4) если известны суммы переменных у и х, используют следующие модификации формул:

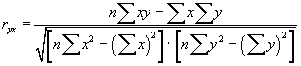
или

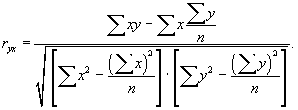
Парный коэффициент корреляции изменяется в пределах от -1 до +1. Абсолютное значение, равное единице, свидетельствует о том, что связь функциональная: -1 ¾ обратная (отрицательная), +1 ¾ прямая (положительная). Нулевое значение коэффициента указывает на отсутствие линейной связи между признаками.

Качественную оценку полученным количественным значениям парных коэффициентов корреляции можно дать на основе шкалы, представленной в табл. 12.1.

Таблица 12.1