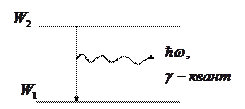10.1. Полная механическая энергия. Система с консервативными силами.
Пусть система тел (материальных точек) перешла по какому-либо пути в потенциальном поле из положения  в положение
в положение 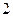 . Чуть раньше было показано, что при перемещении из точки 1 в точку 2 работа силового поля выражается через приращение кинетической энергии:
. Чуть раньше было показано, что при перемещении из точки 1 в точку 2 работа силового поля выражается через приращение кинетической энергии:
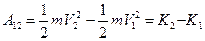 . (10.1)
. (10.1)
С другой стороны, для консервативных сил работа равна убыли потенциальной энергии:
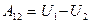 . (10.2)
. (10.2)
Приравнивая выражения (10.1) и (10.2), получаем следующее равенство:
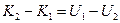 . (10.3)
. (10.3)
Отсюда для замкнутой системы, содержащей произвольное число частиц, получаем
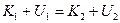 . (10.4)
. (10.4)
Сумма кинетической и потенциальной энергий называется полной механической энергией:
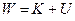 . (10.5)
. (10.5)
Закон сохранения полной механической энергии:
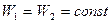 . (10.6)
. (10.6)
В системе лишь с консервативными (и гироскопическими) силами полная энергия остается постоянной (неизменной).
В такой системе могут лишь происходить превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может.
Подчеркнем, что это утверждение справедливо только в инерциальной системе отсчета.
10.2. Система с диссипативными силами.
Пусть в системе наряду с консервативными силами действуют диссипативные силы (например, силы трения). Тогда полную работу всех сил при перемещении системы из точки 1 в точку 2, которая, по-прежнему, равна изменению кинетической энергии, можно записать как:
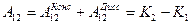 (10.7)
(10.7)
Для консервативных сил имеем:
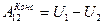 (10.8)
(10.8)
Откуда получаем следующий закон изменения полной механической энергии:
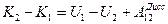
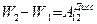 (10.9)
(10.9)
Таким образом, при наличии в системе диссипативных сил полная механическая энергия замкнутой системы уменьшается, т.к. работа диссипативных сил отрицательна.
Пример. Банка с зеленым горошком.
10.3. Излучение квантов. Эффект Мессбауэра.
|
Рассмотрим в качестве иллюстрации применения законов сохранения импульса и энергии эффект
Мессбауэра.
Согласно квантовомеханическим представлениям атомные ядра (или атомы) имеют дискретные уровни энергии. Если ядро (атом) находится в возбужденном состоянии, то затем система переходит в нижнее состояние с испусканием g кванта.
Из закона сохранения энергии, записанного без учета движения ядра:
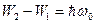 ,
,
где 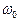 - частота фотона.
- частота фотона.
Однако атом может двигаться, поэтому закон сохранения энергии должен учитывать кинетическую энергию атомов в состояниях 1 и 2 (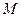 - масса атома):
- масса атома):
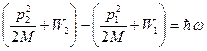 . (10.10)
. (10.10)
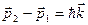 - (10.11)
- (10.11)
импульс, уносимый фотоном.
Здесь 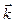 волновой вектор фотона, его модуль - волновое число:
волновой вектор фотона, его модуль - волновое число:
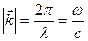 .
.
Выразим 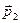 из (10.11) и подставим в (10.10):
из (10.11) и подставим в (10.10):
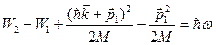 .
.
В рассматриваемом классе задач выполняется условие 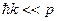 (масса атома
(масса атома 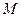 велика, а фотон - безмассовая частица). Поэтому, раскрывая скобки и пренебрегая квадратом фотонного импульса, можем записать
велика, а фотон - безмассовая частица). Поэтому, раскрывая скобки и пренебрегая квадратом фотонного импульса, можем записать
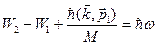 .
.
Итак, величина 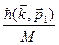 зависит от скорости атома в конечном состоянии и описывает отдачу (откат) атома при испускании
зависит от скорости атома в конечном состоянии и описывает отдачу (откат) атома при испускании 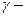 кванта. Отдельные атомы испытывают разную отдачу. Максимальное значение
кванта. Отдельные атомы испытывают разную отдачу. Максимальное значение
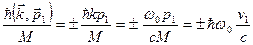 .
.
Поэтому энергия испускаемого кванта определяется выражением
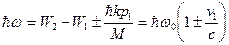 , (10.12)
, (10.12)
где, как следует из опыта, 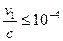 .
.
Т.о., в спектре излучения атомов вместо четко определенной линии на частоте 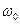 наблюдается уширенная за счет отдачи атому и его движения линия с полушириной
наблюдается уширенная за счет отдачи атому и его движения линия с полушириной
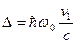 .
.
Минимальное значение, которое удалось получить в газах, составляет 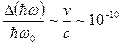 .
.
Идея Мессбауэра (1958 г.).
Р. Мессбауэр (R. Mössbauer) предложил рассматривать атом, помещенный в кристаллическую решетку. Такой атом не участвует в поступательном движении и, более того, отдачу при испускании 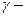 кванта будет испытывать не отдельный атом, а вся решетка, с которой этот атом жестко связан.
кванта будет испытывать не отдельный атом, а вся решетка, с которой этот атом жестко связан.
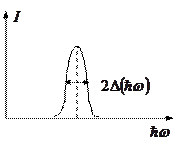
Последнее означает, что значение массы в знаменателе
выражения (10.12) резко возрастает при 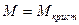 и этой
и этой
дробью с большой точностью можно пренебречь. Тогда
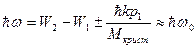 .
.
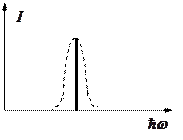 Для кристаллов удалось получить
Для кристаллов удалось получить 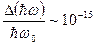 .
.
В 1961 г. немецкому физику Р. Мессбауэру была присуждена
Нобелевская премия по физике.
10.3. Границы движения.
Вернемся опять к системе, в которой действуют только консервативные силы. Для простоты рассмотрим одномерное движение, т.е. перемещение материальной точки осуществляется только вдоль определенной линии (в частности, прямой), а её положение задается одной координатой.
При движении в поле консервативных сил справедлив закон сохранения энергии:
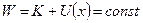 . (10.10)
. (10.10)
Поскольку кинетическая энергия по своему смыслу всегда положительна (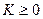 ), то из (10.10) следует, что полная энергия
), то из (10.10) следует, что полная энергия 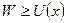 . Это означает, что частица при заданном значении полной механической энергии может находиться только в той области изменения координат и потенциального рельефа, где выполняется условие
. Это означает, что частица при заданном значении полной механической энергии может находиться только в той области изменения координат и потенциального рельефа, где выполняется условие 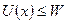 . Условие
. Условие 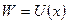 , т.е. равенство полной и потенциальной энергии частицы служит для определения границ её движения.
, т.е. равенство полной и потенциальной энергии частицы служит для определения границ её движения.
Определение: Движение, при котором частица остается в конечной области пространства, называется финитным движением.
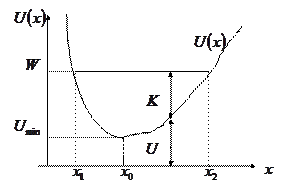 Пример: На рисунке приведена зависимость потенциальной энергии
Пример: На рисунке приведена зависимость потенциальной энергии 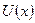 от координаты
от координаты 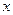 . Прямая
. Прямая 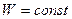 пересекает кривую
пересекает кривую 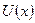 в двух точках с координатами
в двух точках с координатами 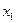 и
и 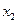 . Т. к. движение частицы возможно лишь в области, где
. Т. к. движение частицы возможно лишь в области, где 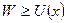 , то точки
, то точки 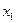 и
и 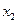 , называемые точками поворота, определяют границы движения. В этих точках полная механическая энергия частицы равна потенциальной
, называемые точками поворота, определяют границы движения. В этих точках полная механическая энергия частицы равна потенциальной 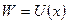 , а кинетическая энергия обращается в нуль (
, а кинетическая энергия обращается в нуль (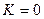 ), т.е. частица останавливается. Минимальной потенциальной энергией и максимальной кинетической энергией частица обладает в
), т.е. частица останавливается. Минимальной потенциальной энергией и максимальной кинетической энергией частица обладает в
точке с координатой 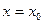 . Справа от точки
. Справа от точки 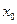 на частицу действует сила, направленная против оси
на частицу действует сила, направленная против оси 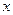 , а слева – по направлению оси, т.е. сила, действующая на частицу, все время направлена к точке
, а слева – по направлению оси, т.е. сила, действующая на частицу, все время направлена к точке 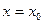 . Это следует из выражения
. Это следует из выражения
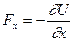 ,
,
согласно которому сила всегда направлена в сторону убывания потенциальной энергии.
В рассмотренном примере частица совершает колебательное движение. Чем больше (выше) полная энергия, тем шире область движения (амплитуда колебаний) точки.
Положение равновесия определяется точкой, где сила, действующая на частицу, обращается в нуль:
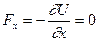 .
.
Если в точке экстремума потенциальная энергия достигает минимума, то равновесие является устойчивым, поскольку возвращающая сила направлена в сторону положения равновесия, и, наоборот, при максимуме потенциальной энергии – равновесие неустойчивое.
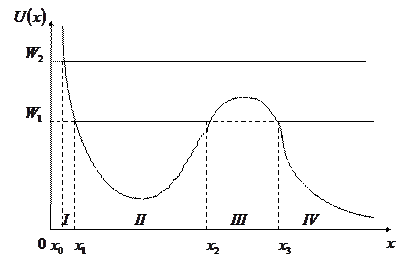 Рассмотрим потенциал более сложной формы. Пусть снова частица движется в одномерном потенциальном поле
Рассмотрим потенциал более сложной формы. Пусть снова частица движется в одномерном потенциальном поле 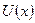 (см. рисунок). Рассмотрим движение частицы с полной механической энергией
(см. рисунок). Рассмотрим движение частицы с полной механической энергией 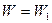 . Прямая
. Прямая 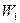 пересекает «потенциальную кривую»
пересекает «потенциальную кривую» 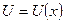 в трех точках
в трех точках 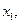
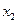 и
и 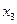 . Движение частицы с энергией
. Движение частицы с энергией 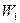 возможно только в областях
возможно только в областях 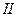 или
или 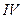 , причем переходить из одной области в другую она не может. Этому препятствует потенциальный барьер в области
, причем переходить из одной области в другую она не может. Этому препятствует потенциальный барьер в области 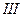 . Частица с энергией
. Частица с энергией 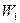 , находящаяся в области
, находящаяся в области 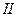 , совершает финитное движение, т.е. движение, происходящее в ограниченной части пространства. Она оказывается запертой в потенциальной яме (область
, совершает финитное движение, т.е. движение, происходящее в ограниченной части пространства. Она оказывается запертой в потенциальной яме (область 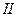 ) и совершает колебания между точками
) и совершает колебания между точками 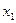 и
и 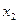 , называемыми точками поворота. Частица, находящаяся в области
, называемыми точками поворота. Частица, находящаяся в области 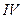 , достигнув точки
, достигнув точки 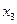 , повернет обратно и будет «уходить на бесконечность». Это инфинитное движение. Для частицы с энергией
, повернет обратно и будет «уходить на бесконечность». Это инфинитное движение. Для частицы с энергией 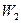 доступна вся область пространства, правее точки
доступна вся область пространства, правее точки 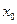 . Её движение является инфинитным. Если значение потенциальной функции
. Её движение является инфинитным. Если значение потенциальной функции 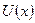 с ростом
с ростом 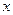 асимптотически приближается к нулю, то скорость частицы на бесконечности равна
асимптотически приближается к нулю, то скорость частицы на бесконечности равна 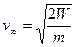 .
.
 2015-10-13
2015-10-13 2782
2782