Консервативные силы.
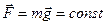 .
.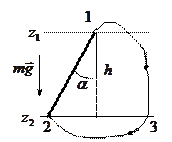
Все силы в макроскопической механике принято делить на консервативные и неконсервативные.
Рассмотрим в качестве примера силу тяжести:
Пусть тело переходит из точки 1, находящейся на высоте 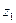 , в точку 2 на высоте
, в точку 2 на высоте 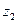 .
.
Вычислим сначала работу силы тяжести вдоль прямой 1-2:
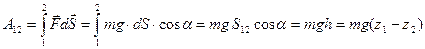
Однако эта же формула оказывается справедливой для вычисления работы силы тяжести и при перемещении вдоль произвольной кривой, например по пути 1-3-2. Это легко увидеть, если разбить путь на маленькие участки, считая их прямолинейными. Тогда работа на таких участках равна:
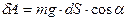 ,
,
где теперь 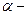 переменный угол. Суммируя по всем участкам и учитывая, что
переменный угол. Суммируя по всем участкам и учитывая, что 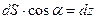 (горизонтальные участки траектории не дают вклада, поскольку на них
(горизонтальные участки траектории не дают вклада, поскольку на них 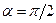 и
и 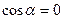 , кроме того, на остальных участках кривой 1-3-2
, кроме того, на остальных участках кривой 1-3-2 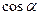 имеет противоположные знаки при движении вверх и вниз, соответственно), получаем то же выражение для работы силы тяжести на всем пути:
имеет противоположные знаки при движении вверх и вниз, соответственно), получаем то же выражение для работы силы тяжести на всем пути:
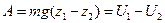 . (8.1)
. (8.1)
Здесь мы ввели функцию 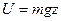 .
.
Из проведенного рассмотрения следует важный вывод: работа силы тяжести не зависит от формы пути, а определяется только начальным и конечным положениями перемещающейся точки.
Определение: Консервативными называются силы, работа которых не зависит от пути перемещения, а определяется только начальной и конечной конфигурациями системы.
Т.о., работа консервативных сил не зависит от пути перехода из начальной в конечную точку траектории. Следовательно, сила тяжести - консервативная сила.
Определение: Р абота консервативных сил по замкнутому контуру равна нулю. 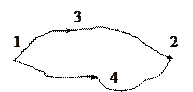
Можно ввести другое определение консервативных сил.
Легко увидеть, что это эквивалентное определение, рассмотрев работу по произвольной замкнутой траектории 1-3-2-4-1. В самом деле, для консервативной силы имеем
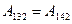
С другой стороны работа меняет знак при изменении направления обхода, т.е. 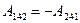 . Тогда и получаем
. Тогда и получаем
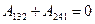 .
.
Поле центральных сил.
Сила называется центральной, если она направлена к одной и той же точке (или от нее) и зависит только от расстояния до этой точки, которую называют силовым центром:
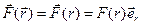 (8.2)
(8.2)
Формула (8.2) действительна в системе координат, начало которой помещено в силовой центр.
Найдем работу центральных сил в случае, когда силовой центр неподвижен.
Элементарная работа в поле центральных сил:
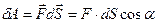
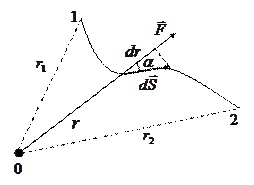
Из рисунка легко видеть, что 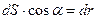 , где
, где 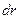 - элементарное приращение длины
- элементарное приращение длины 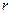 , т.е. расстояния от силового центра 0 до интересующей нас материальной точки. Т.о.,
, т.е. расстояния от силового центра 0 до интересующей нас материальной точки. Т.о.,
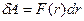 , (8.3) и, поскольку, как предполагается, величина силы
, (8.3) и, поскольку, как предполагается, величина силы 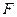 зависит только от расстояния
зависит только от расстояния 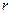 , то элементарная работа также зависит только от абсолютного значения
, то элементарная работа также зависит только от абсолютного значения 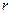 .
.
Соответственно, полная работа выражается определенным интегралом:
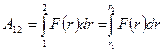 ,
,
значение которого зависит только от расстояний 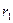 и
и 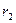 точек
точек 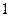 и
и 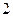 до силового центра
до силового центра 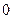 , но не зависит от формы пути, по которому материальная точка перешла из начального положения
, но не зависит от формы пути, по которому материальная точка перешла из начального положения 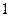 в конечное положение
в конечное положение 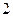 .
.
Поэтому полная работа 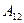 , как и в случае однородной силы тяжести, может быть записана также в виде:
, как и в случае однородной силы тяжести, может быть записана также в виде:
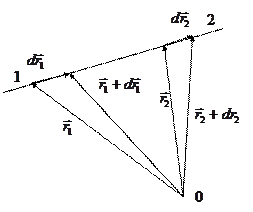
Обозначим посредством 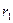 и
и 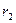 радиус-векторы точек
радиус-векторы точек 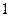 и
и 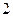 , проведенные из неподвижного начала
, проведенные из неподвижного начала 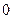 .
.
В общем случае могут перемещаться как материальная точка 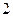 , так и силовой центр
, так и силовой центр 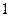 , причем силы
, причем силы 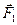 и
и 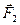 их взаимодействия подчиняется третьему закону Ньютона:
их взаимодействия подчиняется третьему закону Ньютона: 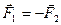 и направлены вдоль прямой
и направлены вдоль прямой 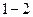 , соединяющей частицы (см. рисунок).
, соединяющей частицы (см. рисунок).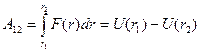 . (8.4)
. (8.4)
Тогда элементарную работу 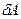 можно записать как:
можно записать как:
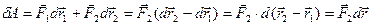 .
.
Здесь 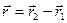 есть радиус-вектор точки
есть радиус-вектор точки 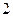 относительно точки
относительно точки 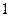 .
.
Следовательно, как при вычислении элементарной, так и полной работы силовой центр 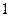 может считаться неподвижным, а точка
может считаться неподвижным, а точка 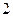 – перемещающейся относительно него. Поскольку сила
– перемещающейся относительно него. Поскольку сила 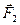 направлена по вектору
направлена по вектору 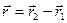 , то работа, по-прежнему определяется выражениями:
, то работа, по-прежнему определяется выражениями:
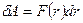 и
и 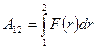 .
.
Сюда входят только расстояние между взаимодействующими точками и его приращение.
Выводы: работа центральных сил не зависит от пути перехода. Все центральные силы консервативны. Пример. К центральным относятся силы гравитационного 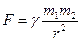 и кулоновского
и кулоновского 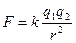 взаимодействий.
взаимодействий.
Неконсервативные силы.
К неконсервативным силам относятся все остальные силы, кроме рассмотренных выше консервативных. Среди неконсервативных сил выделяют диссипативные и гироскопические.
1) Диссипативные силы.
Определение: диссипативными называются такие силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна.
Силы трения (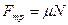 ) и сопротивления (для жидкостей и газов
) и сопротивления (для жидкостей и газов 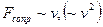 ). Важно, что для замкнутой системы работа диссипативных сил всегда отрицательна, поскольку направление силы всегда противоположно направлению перемещения или скорости.
). Важно, что для замкнутой системы работа диссипативных сил всегда отрицательна, поскольку направление силы всегда противоположно направлению перемещения или скорости.
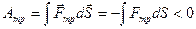
Примечание: для незамкнутой системы сила трения может быть источником движения.
Гироскопические силы зависят от скорости движения материальной точки и действуют перпендикулярно этой скорости. Работа этих сил всегда равна нулю. Например, гироскопическими силами являются сила Лоренца (магнитная)
в системе СИ: 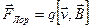 ,
,
в системе СГС: 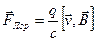 ,
,
и сила Кориолиса
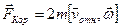 .
.
 2015-10-13
2015-10-13 17477
17477
