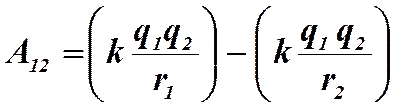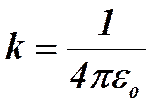
Для работы кулоновских сил можно получить аналогичную формулу

;

Покажем, что сила упругости также является консервативной силой. Ее работа вычисляется по формуле

.

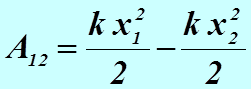В самом деле, элементарная работа силы упругости равна

.

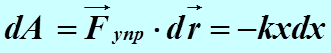После интегрирования получим

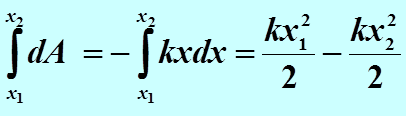
Как видим, работа консервативной силы всегда может быть представлена разностью двух слагаемых, характеризующих начальную и конечную точки траектории:

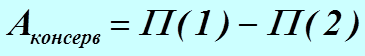
Эти слагаемые представляют собой потенциальную энергию взаимодействующих тел в указанных состояниях. Это значит, что потенциальная энергия, связанная с гравитационным взаимодействием двух тел будет равна

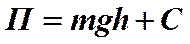или в общем случае .

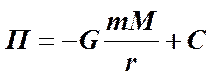Потенциальная энергия двух взаимодействующих электрических зарядов будет равна .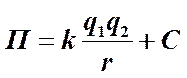

Потенциальная энергия деформированной пружины определится соотношением 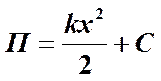. Следует заметить, что потенциальная энергия определяется с точностью до произвольной постоянной 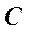, величина которой определяется из соображений удобства. Обычно ее принимают равной нулю.

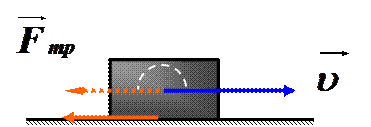Покажем, что сила трения не является консервативной силой. Для этого подсчитаем работу силы трения скольжения, действующей на брусок, движущийся по горизонтальной поверхности.

, , ,

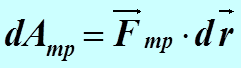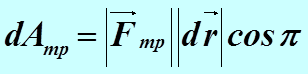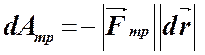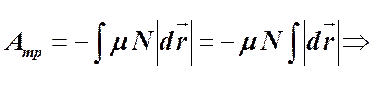
Как видим, работа силы трения зависит от вида траектории (от ее длины) и в случае замкнутой траектории не равна 0.