2015-10-13
585
Основні положення класичної термодинаміки, що розглянуті у попередніх розділах, описують закономірності, які виникають в системі при встановленні рівноваги. При цьому, як підкреслювалося раніше, будь-яка точка системи характеризується постійними температурою і тиском. Гетерогенна система, окрім цього, характеризується рівністю хімічного потенціалу атомів даного компоненту в усіх фазах.
Відмінною особливістю основних законів термодинаміки є відсутність в них параметру часу і похідних незалежних параметрів стану у часі. Це й зрозуміло: стани рівноваги мають властивості не змінюватися до тих пір, доки зовнішні умови є незалежними. Саме цьому класична термодинаміка, яка розглядає лише рівноважні, класичні ситуації, не надає можливості проведення фізико-хімічного аналізу процесів фазових переходів і є, по-суті, термостатикою.
В останні десятиріччя були зроблені багато чисельні спроби побудови термодинаміки незворотних процесів. У дійсний час розвивається декілька підходів до опису динаміки процесу фазових переходів. В них використовуються різні за своєю природою простори уявлень. Один з них – фазовий простір Гіббса – обговорювався раніше. Можливими є й інші простори уявлень – простір «подій», простір «імпульсу і енергії», простір «станів», простір «станів і енергії» і інші. Частина цих просторів – скалярні, інші – векторні. Еволюція системи при фазовому переході описується деякою єдиною траєкторією фігуративної точки. Параметри траєкторії задаються конкретними умовами процесу.
Один з найважливіших напрямків розвитку термодинаміки незворотних процесів базується на останніх досягненнях макроскопічної теорії явищ переносу [3]. До цих досягнень відносять феноменологічні (тобто експериментально встановлені) закони:
- закон теплопровідності Фур’є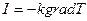 
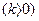про пропорційність теплового потоку градієнту температури;
- закон дифузій Фіка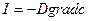 
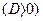про пропорційність потоку атомів компоненту градієнту концентрації;
- закон Ома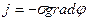 
про пропорційність щільності току j градієнту потенціалу j;
- закон Ньютона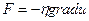 
про пропорційність сили внутрішнього тертя F градієнту швидкості u і т.і.
Причини, що викликають незворотні явища, носять назву «сили» і позначаються через Хі (і=1, 2, …): градієнт температури, градієнт концентрації і т.д. Кількісні характеристики незворотних явищ, що викликані силами Хі, називаються «потоками» Ii (i=1, 2, …): потік теплоти, потік атомів, що дифундують, і т. ін.
Фізичні потоки представляють собою швидкості зміни відповідних параметрів стану (температури, концентрації і т. ін.).
Як бачимо, в термодинаміці незворотних процесів параметр «швидкість» враховує фактор часу.
Грунтуючись на законах класичної термодинаміки і явищ переносу, термодинаміка незворотних процесів базується на трьох основних принципах.
1. Стан локально рівноважних частин системи визначається основним рівнянням термодинаміки для квазистатистичних процесів:
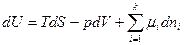(19)
Загальна зміна ентропії системи аддитивно складується зі змін в окремих її частинах. Локальна швидкість виникнення ентропії має вигляд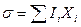 
, де Ii – потік; Хі – сила.
2. Потік Ii, що викликаний дією сил Хк –, є пропорційним цим силам:
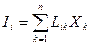(і=1, 2, … n) (20)
Коефіцієнти Lik називають класичними.
3. При відповідному виборі потоків Ii та Хі матриця кінетичних коефіцієнтів є симетричною (співвідношення взаємності Онзагера):
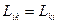(i, k=1, 2, … n) (21)
Це означає, що якщо градієнт температури викликає градієнт концентрації, то й градієнт концентрації при деякому процесі викликає градієнт температури.
Наведені три принципи термодинаміки незворотних процесів утворюють самоузгоджену систему рівнянь для визначення спряжених потоків Ii та Хі.
Аналіз фазових переходів з допомогою принципів термодинаміки незворотних процесів базується поперед усього на понятті локальної рівноваги. Відомо, час встановлення термодинамічної рівноваги зростає зі збільшенням розміру системи. Тому можна вважати, що в малих макроскопічних об’ємах рівновага встановлюється значно раніше, ніж між цими об’ємами. З цього виходить, що хоча система в цілому і не знаходиться в рівновазі, в невеличких частинах її рівновага вже встановилася при певних параметрах: температурі, тиску, хімічному потенціалі атомів компонентів. При цьому важливо, щоб в малих частинах системи було ще багато часток, а також щоб відхилення від рівноваги були невеликими.
Конкретизуємо ці положення на прикладі розглядання фазового переходу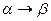 
. Знаючи вихідний склад материнської фази a 
при температурі Т1, а також рівноважні концентрації обох фаз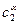 
і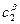 
при температурі Т2 (знаходяться на діаграмі стану), можна знайти напрямок та величину потоку дифузії атомів компонентів. Для цього припустимо, що рівноважні значення концентрацій для фаз 
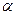і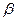 
при Т2 (температурі фазового переходу) встановилися тільки в невеликих об’ємах цих фаз, які примикають до фазової границі 
.
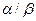Оскільки процес фазового переходу продовжується невеликий час, очевидно, що ділянки материнської 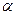-фази, які віддалені від границі 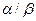, ще не встигли змінити концентрацію.
Таким чином, у припущенні, що дифузія в системі є вирівнюючою і з врахуванням знаку нерівності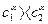 
з’являється можливість визначити напрямок дифузії атомів компоненту Б в 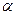-фазі, а обчисливши 
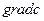(у припущенні, що відома величина D при даній Т2) – визначити величину дифузійного потоку І атомів компоненту Б.
При цьому можливі два випадки.
1. Дифузійний потік І атомів компоненту Б в 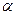-фазі направлений до границі 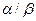( 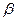-фаза побудована в основному з атомів компоненту Б). Пересичення 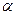-фази компонентами Б, що виникає, приводить до пересування 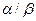границі всередину 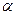-фази, тобто приведе до росту кристалів 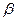-фази.
2. Дифузійний потік І атомів компоненту Б в 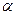-фазі направлений від границі 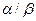. У результаті склад 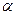-фази на границі 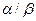обідниться по відношенню до рівноважного. Для підтримання рівноваги атоми Б з 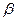-фази будуть переходити до 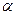-фази до тих пір, доки рівноважна концентрація 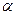-фази на між фазній границі не відновиться. Природно, що це приведе до часткового розчинення кристалів 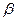-фази.
Описана схема аналізу фазового переходу 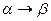дозволяє не тільки визначити стимулюючий направлену дифузію атомів компонентів градієнт концентрації як рушійну силу процесу, а й спрогнозувати кінцевий результат процесу (розчинення або виділення 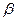-фази).
