Математическое моделирование в экологии

Остановимся на некоторых понятиях. Под особью понимается отдельный индивидуум, отдельный организм. Популяция - это совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию. И, наконец, сообщество - это совокупность совместно сосуществующих популяций.

Рассмотрим примеры моделей взаимодействия популяций:

1. МОДЕЛИ ВНУТРИВИДОВОЙ КОНКУРЕНЦИИ.

Данная модель может быть выражена уравнением:

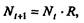
в которой численность популяции в момент времени t равна N, и изменяется во времени пропорционально величине основной чистой скорости воспроизводства R.

Решение которого имеетвид

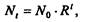
где N₀- начальная численность популяции. Эта модель, однако, описывает популяцию, в которой отсутствует конкуренция и в которой R является константой; если R>1, то численность популяции будет бесконечно увеличиваться.[3]

Конкуренцию можно определить как использование некоего ресурса (пищи, воды, света, пространства) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией, если же они относятся к разным видам, то их взаимоотношения называют межвидовой конкуренцией.

2. МОДЕЛЬ «ХИЩНИК-ЖЕРТВА» (МОДЕЛЬ ВОЛЬТЕРРА).

Первыми экосистемами, которые изучались с помощью количественных методов, были системы «хищник – жертва». Американец А. Лотка в 1925 году и итальянец В. Вольтерра в 1926 году создали математические модели роста отдельной популяции и динамики популяций, связанных отношениями конкуренции и хищничества. Исследование систем «хищник – жертва» показало, что типичной для популяции жертв эволюцией является увеличение рождаемости, а для популяции хищников – совершенствование способов ловли жертвы.

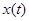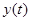Пусть и – численность жертв и хищников соответственно. Предположим, что

· единственным фактором, ограничивающим размножение жертв, является давление на них со стороны хищников,

· а размножение хищников ограничивается количеством добытой ими пищи (количеством жертв).

Тогда в отсутствие хищников численность жертв должна расти экспоненциально с относительной скоростью α, а численность хищников в отсутствие жертв – также экспоненциально убывать с относительной скоростью β; α и β – коэффициенты естественного прироста жертв и естественной смертности хищников, соответственно.

Пусть 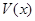– количество (или биомасса) жертв, потребляемых одним хищником за единицу времени, причем k-я часть полученной с этой биомассой энергии расходуется на воспроизводство, а остальная тратится на поддержание основного обмена. Тогда уравнения системы хищник-жертва можно записать в виде

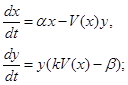(1)

функцию V(x) обычно называют трофической функцией хищника и именно ее определяют в экспериментальных работах. В настоящее время считается установленным, что эта функция принадлежит одному из представленных на рисунке 2 типов:

· I - характерен для беспозвоночных и некоторых видов хищных рыб;

· II - для хищников-фильтраторов (например, многих моллюсков);

· III - для позвоночных – организмов, проявляющих достаточно сложное поведение (например, способных к обучению). Аналогичный вид имеет трофическая функция, если жертвы могут вырабатывать защитную стратегию.

При малых значениях x, когда почти все жертвы становятся добычей хищника, который всегда голоден и насыщения у которого не наступает (ситуация довольно обычная в природе), трофическую функцию V(x) можно считать линейной функцией численности жертв, т.е. V(x) = mx. Кроме того, предположим, что k = const. Тогда

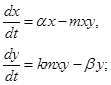(2)

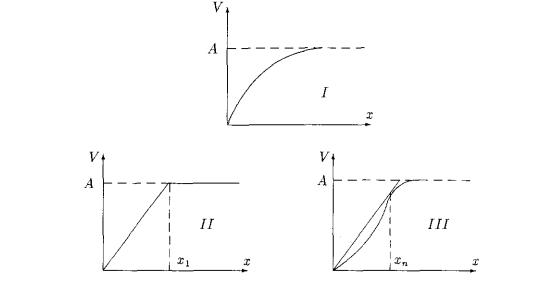
Рисунок 1. Характерные типы трофической функции хищника.

Система (2) – классическая модель хищник-жертва Вольтерра, который показал, что эта система имеет интеграл

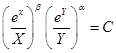(3)

(следует из уравнения 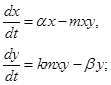, в котором переменные разделяются). Здесь 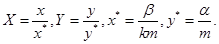Если 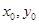– начальные значения численности жертв и хищников соответственно, то

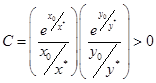
и уравнение (3) описывает семейство вложенных друг в друга замкнутых кривых (рис. 3), соответствующих фазовым траекториям периодических решений системы (2). Заметим, что при увеличении C амплитуды колебаний x и y возрастают. При минимальном значении 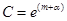эти кривые стягиваются в точку с координатами 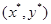. Очевидно, что точка 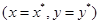является стационарным решением 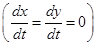системы (2). Если в некоторый момент времени 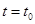, искомые переменные принимают значения 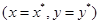, то и во все последующие моменты времени эти равенства сохраняются. Кроме того, стационарным является тривиальное решение x=0, y=0. Других стационарных решений система (2) не имеет.

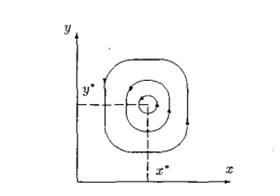
Рисунок 2. Фазовые траектории решений уравнений системы хищник-жертва

Хотя модель Вольтерра смогла объяснить многие реально наблюдавшиеся явления, есть у нее большой недостаток – при любых сколь угодно слабых возмущениях фазовых координат система переходит из одного цикла в другой.