Модель системы «хищник-жертва»

Рассмотрим изолированную от прочих сторонних воздействий экологическую систему, в которой существуют два вида – «хищник» и «жертва». При этом в данной экологической системе для «жертвы» имеется неограниченное количество корма, «жертва» размножается естественным путем, а ее смертность обусловлена только воздействием со стороны «хищника», причем «жертва» является единственным источником пищи для «хищника». В отсутствие «жертв» «хищники», естественно, вымирают.[5]

Обозначим через 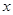количество «жертв», а через 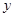– количество «хищников». Тогда динамика взаимодействия между «жертвой» и «хищником» описывается следующей системой дифференциальных уравнений:

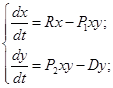
Первое уравнение отражает закономерность изменения популяции «жертв», а второе «хищников». Слагаемое 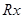характеризует скорость размножения «жертв» в отсутствие «хищника», а слагаемое 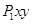характеризует скорость гибели «жертв» за счет их уничтожения «хищниками»; скорость этого процесса пропорциональна количеству парных встреч. Слагаемое 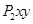характеризует увеличение численности «хищников» за счет поедания «жертв», а слагаемое 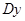характеризует естественную смертность «хищников», в отсутствие пищи, т. е. «жертв». Коэффициенты уравнения 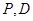и 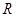представляют собой константы, имеющие только положительные значения. Представленную систему уравнений называют уравнениями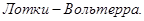

Применив метод неопределенных масштабов, преобразуем переменные к безмерному виду:

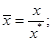
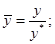
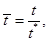
где 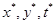- неопределенные масштабные множители. Используя эти безмерные соотношения, получим:

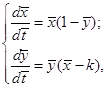
где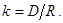

В результате преобразования система уравнений вместо четырех параметров содержит только один – отношение коэффициентов смертности и рождаемости, которое, как оказывается, и определяет взаимодействие «хищников» и «жертв». Естественно, для полной определенности данная система уравнений должна быть дополнена начальными условиями:

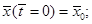
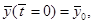
т. е. количество «жертв» и «хищников» в начальный момент времени, которые вместе с коэффициентом к являются параметрами 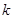задачи.

Анализ данной системы уравнений показывает, что она имеет устойчивое стационарное решение при начальных условиях

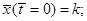
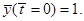
Малые начальные отклонения от этого состояния порождают почти синусоидальные гармонические колебания неизменной амплитуды. Другое, но уже неустойчивое стационарное состояние соответствует начальным условиям

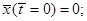
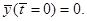
Здесь любое малое отклонение от этого состояния приводит к развитию нелинейных колебаний в системе.

Несмотря на ряд недостатков, модель Лотки—Вольтерра для математической экологии считается базовой, при помощи этой простой модели были установлены некоторые качественные закономерности, в частности, колебание численности видов.

Для реализации модели системы «хищник - жертва» мы будем использовать пакет моделирования MVS.

Рассмотрим две модели сначала модель Лотки-Вольтерра, а затем уточненную модель Базыкина.