2015-10-14
572
Предполагается, что теплообмен происходит только между двумя теплоносителями через поверхность змеевика F3.
Уравнение теплового баланса змеевика:
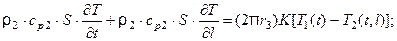
где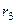 
- радиус змеевика.
Температура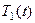 
в резервуаре изменяется только во времени и определяется из уравнения теплового баланса для проточной емкости, в которой учитывается распределенный источник 
:
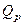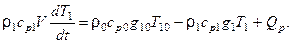
Количества тепла Qp, передаваемого через стенки змеевика (распределенный по длине змеевика источник), вычисляется по формуле:
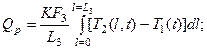
где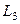 
-длина змеевика; 
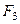-поверхность теплообмена змеевика.
После некоторых преобразований уравнения нестационарной модели теплообменника «смешение – вытеснение» принимают следующую форму:
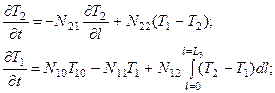
где
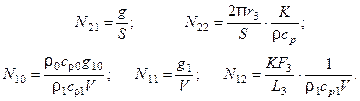
Как обычно, для решения системы на ЭВМ используется метод конечных разностей по геометрической координате; уравнение с частными производными аппроксимируется системой обыкновенных дифференциальных уравнений. Замена дифференциала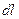 
на разность 
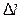приводит к тому, что во втором уравнении системы интеграл заменяется конечной суммой, в которой число слагаемых обусловлено числом участков разбиения змеевика:
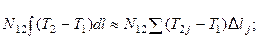
где m – число участков разбиения, или число ячеек идеального перемешивания змеевика;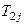 
- температура на выходе 
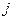-той ячейки змеевика.
Решение системы уравнений будет однозначным, если известны: коэффициенты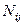 
при i=1, 2; j=0,1,2; граничные условия для теплоносителей на входе 
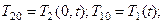начальные условия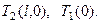 
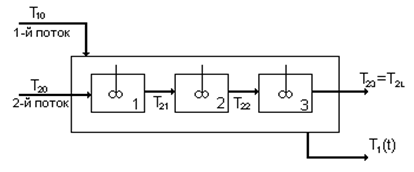
На рисунке 1.2 приведена схема теплообменника типа «смешение– вытеснение», где змеевик представлен цепочкой из трех последовательно соединенных ячеек перемешивания; здесь же указаны все условные обозначения, используемые при записи уравнений в конечных разностях. В соответствии с числом ячеек перемешивания подготовим систему уравнений к моделированию на ЭВМ:
для первой ячейки перемешивания:
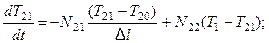
для второй ячейки:
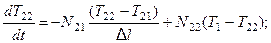
для третей ячейки:
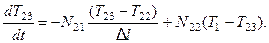
для резервуара:
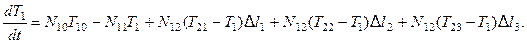
Если участки разбиения одинаковы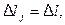 
предыдущие уравнение можно записать в виде следующей системы:
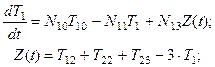
где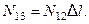 
Правые части уравнения моделируются почленно, т.е. после раскрытия скобок, что позволяет построить структурную схему без промежуточных сумматоров.
Модель реализована с помощью пакета визуального программирования SIMULINK Matlab (Рисунки 1.3-1.9).
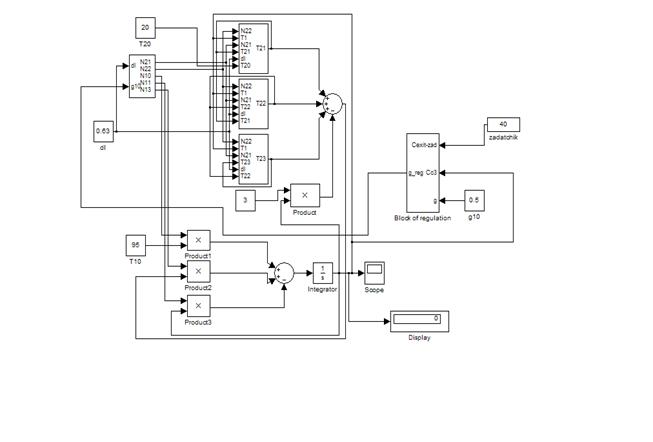
Рисунок 1.3 – Модель системы регулирования теплообменника
«смешение - вытеснение»
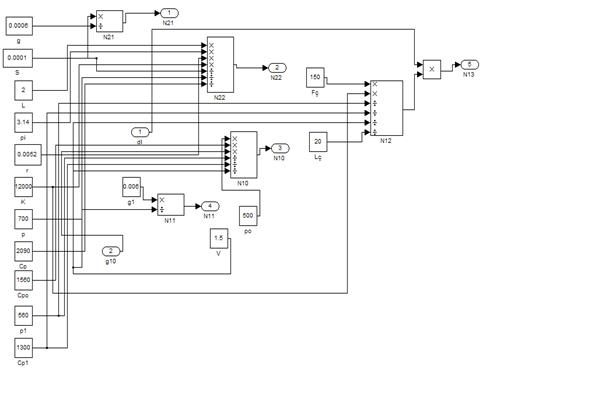
Рисунок 1.4 – Подсистема исходных данных
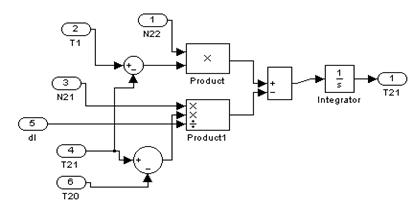
Рисунок 1.5 – Подсистема для первой ячейки перемешивания
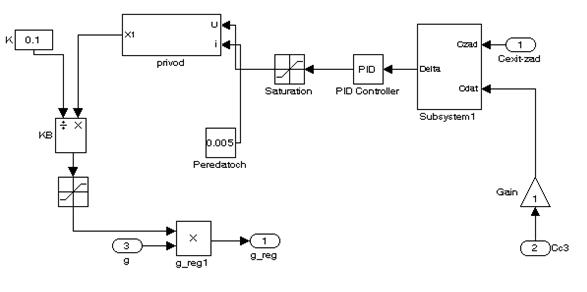
Рисунок 1.6 – Подсистема блока регулирования теплообменника «смешение - вытеснение»
 |
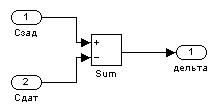Рисунок 1.7 – Подсистема блока сравнения
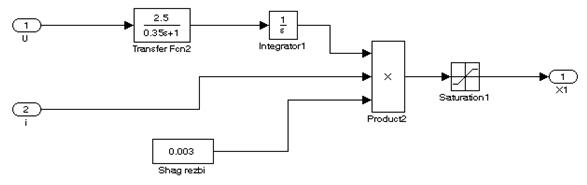
Рисунок 1.8 – Подсистема управляющего привода (ИУ)
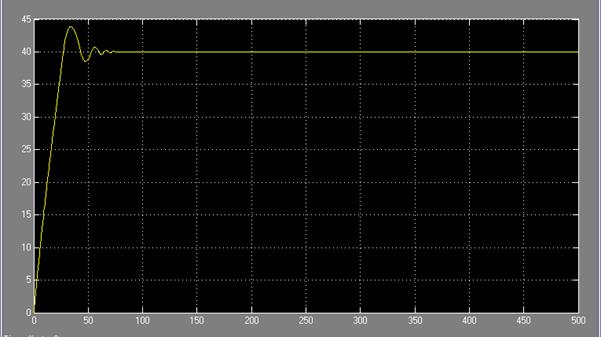
Рисунок 1.9 – График зависимости температуры
Заключение
В данном курсовом проекте были рассмотрены и смоделированы в с помощью пакета визуального программирования SIMULINK пакет Matlab следующие модели систем регулирования объектов химической технологии: проточная гидравлическая ёмкость переменного объёма; адиабатический теплообменник – смеситель переменного объёма; каскад химических реакторов полного перемешивания.
Представлены графики зависимости регулируемых величин в зависимости от времени.
Список используемых источников
1 Луценко В.А., Финякин Л.Н. Аналоговые вычислительные машины в химии и химической технологии. – М.: Химия, 1979 – 248 с.
2 Машины и аппараты химических производств. Под ред. И.И. Чернобыльского. – М.: Машиностроение, 1974. – 456 с.
