2015-10-14
431
Процесс истечения жидкости в этом случае является нестационарным, т.е. скорость истечения переменна во времени. За бесконечно малый промежуток времени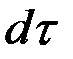 
из сосуда (рис. 4.5) вытекает жидкость объемом 
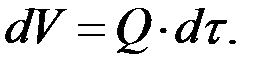Из этого условия с учетом (4.6) получим:
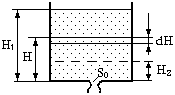Рис. 4.5. Схема истечения жидкости из сосуда при переменном
ее уровне
|
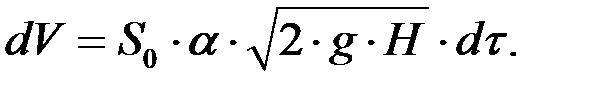(4.7)
Уровень жидкости в сосуде при этом понизится на величину dH, поэтому можно записать:
,
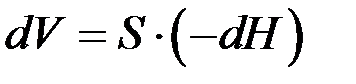где S – площадь поперечного сечения аппарата. В нашем случае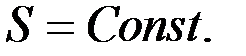 
Знак минус в этом выражении указывает на уменьшение уровня жидкости при истечении. Теперь получим:
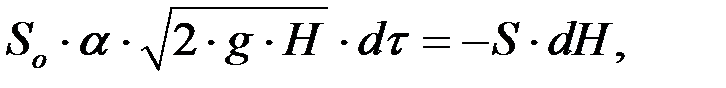(4.8)
отсюда найдем:
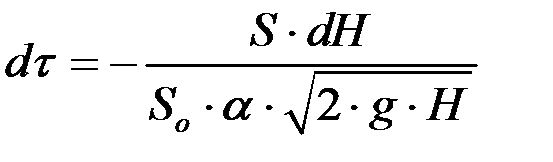. (4.9)
Проинтегрируем (4.8) при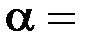 
Const:
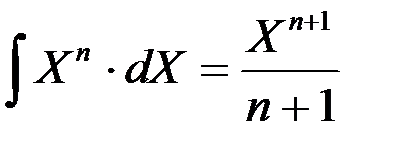. (4.10)
Поменяв местами пределы интегрирования, получим:
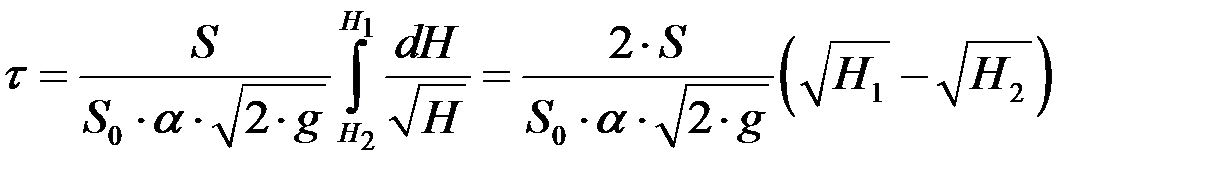. (4.11)
Уравнение (4.10) позволяет рассчитать время истечения из аппарата жидкости объемом 
.
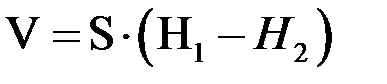Продолжительность истечения из резервуара всей жидкости получим из (4.11) при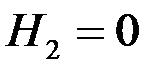 
:
t =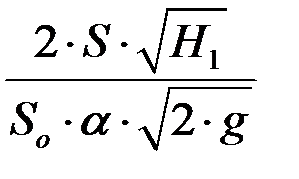 
(4.12)
или
t =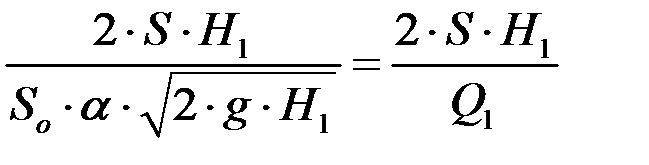 
. (4.13)
Числитель в уравнении (4.12) – удвоенный объем резервуара; знаменатель – секундный расход Q 1 в начальный момент истечения жидкости, т.е. при уровне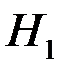 
. Следовательно, время опорожнения аппарата в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному Н 1. Если жидкость в аппарате находится под давлением Р о, то уравнение (4.9) приобретает вид:
.
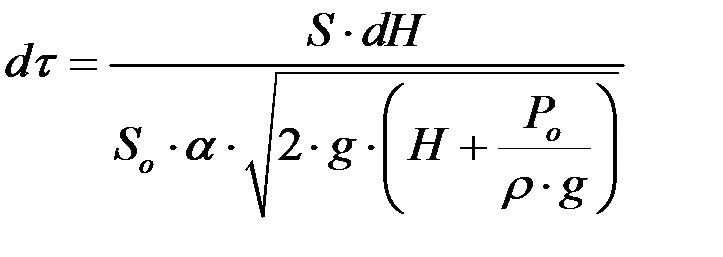Отсюда получим:
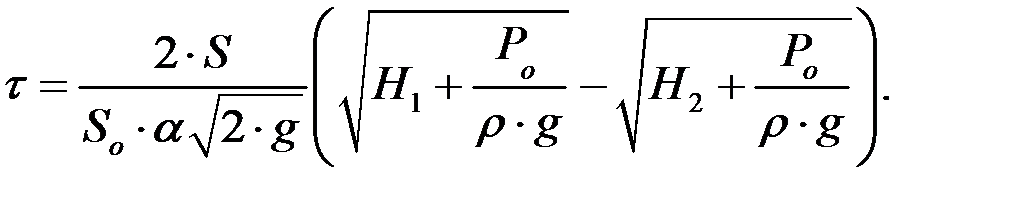(4.14)
t =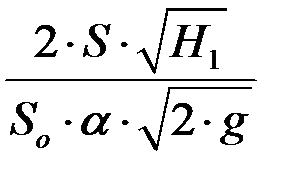 
(4.15)
или
t =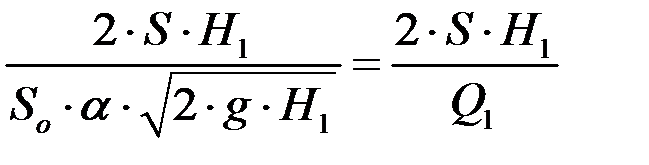 
. (4.16)
