2015-10-14
378
Одной из важнейших задач практической гидравлики, без решения которой использование уравнения Бернулли невозможно, является количественное определение потерь напора для любого случая.
В гидравлике различают два вида сопротивлений:
1. Сопротивления сил вязкостного трения частиц жидкости друг с другом и с ограничивающими стенками пропорциональны длине потока. Соответствующие им потери напора (потери по длине) обозначаются через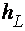 
.
2. Местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (колено, соединение трубопроводов, дроссель, клапан и др.), которые приводят к изменениям величины или направления скорости течения жидкости. Соответствующие им потери напора (местные потери) обозначаются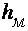 
.
Поэтому полные потери напора между двумя сечениями потока при наличии сопротивлений обоих видов будут равны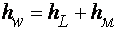 
.
При движении жидкости на прямых участках трубопровода потери напора по длине потока, выраженные в метрах столба жидкости, определяются по формуле Дарси−Вейсбаха
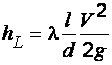, (2.10)
где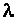 
– коэффициент гидравлического трения (коэффициент Дарс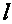и); 
и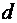 
– длина и диаметр трубопровода; 
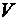– средняя скорость потока.
Данная формула справедлива как для ламинарного, так и для турбулентного режимов движения, но для каждого из этих случаев течения жидкости существуют свои зависимости для определения коэффициента .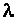
Безразмерный коэффициент гидравлического трения 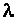учитывает влияние на потери напора по длине всех факторов, которые не нашли отражения в формуле (2.10), но существенны для гидравлических сопротивлений. Важнейшими из этих факторов является вязкость жидкости и состояние стенок трубопровода.
Как показали экспериментальные исследования, на потери напора существенное влияние оказывает шероховатость поверхности, которая количественно оценивается средней высотой выступов, измеряемой в линейных единицах, и называется абсолютной шероховатостью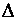 
.
При турбулентном режиме в зависимости от соотношения 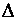и толщины ламинарного слоя 
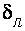, образующегося непосредственно у стенок трубы, могут быть выделены три зоны гидравлических сопротивлений: 1) зона гидравлически гладких труб при 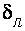> 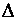, когда выступы шероховатости покрыты ламинарным слоем; 2) зона неполной шероховатости при 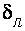= 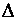, когда выступы шероховатости того же порядка, что и толщина ламинарного слоя; 3) зона полной шероховатости (квадратичная) при 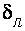< 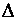, когда выступы шероховатости не сглаживаются полностью ламинарным слоем.
Однако оценка шероховатости только по высоте выступов недостаточна, поскольку она не учитывает характер расположения и форму выступов. Поэтому было введено понятие эквивалентной шероховатости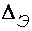 
, т. е. такой условной равномерной шероховатости, которая дает при подсчете одинаковую с фактической шероховатостью величину коэффициента гидравлического трения 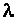и которая определяется по формуле
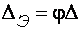, (2.11)
где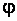 
– коэффициент, определяющий характер расположения выступов и их форму.
При нахождении потерь напора по длине необходимо предварительно выявить зону, а затем по соответствующим формулам определять коэффициент гидравлического трения .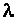
I. Зона ламинарного режима (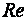 
<2 320)
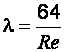. (2.12)
При подстановке данного выражения в формулу (2.10) с учетом равенства (2.7) получается формула Пуазейля:
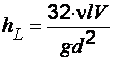. (2.13)
Данная формула показывает, что потери напора по длине при ламинарном режиме прямо пропорциональны средней скорости движения в первой степени и не зависят от состояния внутренней поверхности стенок трубы.
II. Переходная зона (2 320< 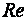<4 500)
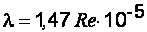– формула Никурадзе. (2.14)
