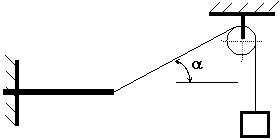
Однородная балка массой m жёстко заделана в вертикальную стену. Длина балки L. Вес балки P. К концу балки закреплена нить, переброшенная через неподвижный блок. На нити закреплён груз весом P. Угол наклона нити к горизонту α. Определить реакции, возникающие в жёсткой заделке.
Будем решать это простейшую задачу строго следуя выше изложенной методике.
Поскольку условие нам понятно а эскиз уже готов, начнём с пункта 3 и приложим активные нагрузки. Они представлены двумя силами - сила тяжести балки G и весом груза P. Ясно что вес груза натягивает нить, которая в свою очередь воздействует на балку силой T=P. Обозначим на рисунке активные силы зелёным цветом.
Поскольку в задаче требуется найти реакции в жёсткой заделке (точка А) будем рассматривать равновесие балки. В ведём систему координат XY.
Заменим действие жёсткой заделки на балку реакциями Rx, Ry и реактивный момент М.
Таким образом мы получаем плоскую произвольную систему сил, приложенных к выбранному нами объекту равновесия - балке.
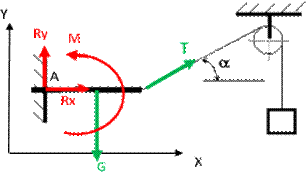
Для такой системы сил можно составить три уравнения равновесия.
Сумма проекций всех сил на координатную ось Х:
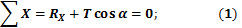
Сумма проекций всех сил на координатную ось Y:
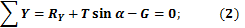
Сумма моментов относительно точки А. Эту точку выбираем для составления суммы моментов потому, что в ней пересекаются две неизвестные силы Rx и Ry:
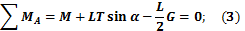
Поскольку в полученной системе из трёх уравнений содержится четыре неизвестных записываем четвёртое уравнение, известное нам из курса физики (g - ускорение свободного падения):

Для нахождения неизвестных достаточно решить полученную систему уравнений, что с точки зрения алгебры не представляет никакой сложности.
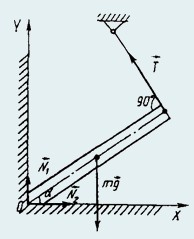
21. Однородный стержень ОА упирается одним концом в угол и удерживается за другой конец нитью (рис.). Масса стержня m, а угол его наклона к горизонту равен α. Найти силу натяжения нити, а также силы, с которыми стержень давит на пол и на стену.
Решение.
На стержень действуют четыре силы: сила тяжести mg, сила натяжения нити Т, силы нормальных реакций пола N1 и стены N2.
Так как стержень находится в равновесии, то
mg + T + N1 + N2 = 0. (векторно)
Суммы проекций этих сил на оси ОХ и OY равны нулю:
N2 − Tsinα = 0, (1)
N1 − mg + Tcosα = 0. (2)
Составим уравнение для моментов сил относительно оси, проходящей через точку А:
(1/2)mglcosα − Tl = 0,
где l − длина стержня.
Из этого уравнения найдем
T = (1/2)mgcosα.
Подставим это значение в уравнения (1) и (2):
N2 = mgsin2α, N1 = mg(1 + sin2α)/2.
Согласно третьему закону Ньютона, с такими по модулю силами давит стержень на стену и пол.
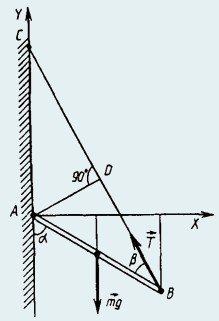
22. Однородный стержень АВ прикреплен к вертикальной стене посредством шарнира А и удерживается под углом α = 60° к вертикали с помощью невесомой веревки ВС, образующей с ним угол β = 30° (рис.). Определить силу натяжения веревки, а также модуль и направление силы реакции шарнира, если известно, что масса стержня m = 2,0 кг.
 Решение.
Решение.
На стержень действуют следующие силы: сила тяжести mg, приложенная к середине стержня и направленная вертикально вниз; сила натяжения веревки Т, приложенная в точке В и направленная вдоль веревки; сила реакции шарнира N. Модуль и направление силы N неизвестны, поэтому на рисунке она не показана.
Запишем условие равновесия в векторной форме:
mg + T + N = 0,
а затем в проекциях на оси ОХ и OY:
Nx − Tsin(α − β) = 0, (1)
Ny − mg + Tcos(α + β) = 0. (2)
Составим уравнение для моментов сил относительно оси, проходящей через точку А:
(l/2)mgsinα − Tlsinβ = 0, (3)
где l − длина стержня.
Из уравнений (1) и (2) найдем:
Nx = Tsin(α − β), Ny = mg − Tcos(α − β).
Модуль силы N
N = √{Nx2 + Ny2} = √{(Tsin(α − β))2 + (mg − Tcos(α − β))2} = √{T2 + m2g2 − 2mgTcos(α − β)}. (4)
Из уравнения (3) следует:
T = mgsinα/(2sinβ), T = 17 H.
Подставив полученное выражение Т в формулу (4), после преобразований и вычислений получим:
N = mg√{1 + sin2α/(4sin2β) − sinαcos(α − β)/sinb}, N = 9,8 H.
Направление вектора N определяется углом γ, который этот вектор составляет с осью ОХ. По значениям проекций Nx и Ny найдем
tgγ = Nx/Ny = (mg − Tcos(α − β))/(Tsin(α − β)).
Подставив сюда
Т = mgsinα/(2sinβ),
получим после преобразований:
tgγ = (2sinβ − sinαcos(α − β))/(sinαsin(α − β)), tgγ = √3/3, γ = 30°.
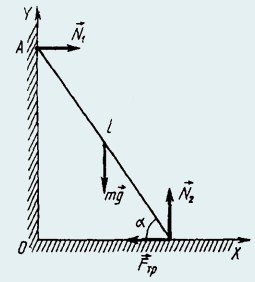
23. Лестница опирается одним концом о вертикальную гладкую стену, а другим − о землю. Коэффициент трения лестницы о землю μ = 0,4. Центр тяжести лестницы находится на ее середине. Определить наименьший угол α, который лестница может образовать с горизонтом, не соскальзывая.
Решение.
На лестницу действуют сила тяжести mg, силы нормальных реакций N1 и N2 стены и земли, сила трения Fmp (рис.).
Лестница находится в равновесии, следовательно,
mg + N1 + N2 + Fmp = 0,
поэтому суммы проекций всех сил на оси ОХ и OY равны нулю:
N1 − Fmp = 0,
N2 − mg = 0,
или
N1 − μN2 = 0, (1)
N2 − mg = 0. (2)
Пусть l − длина лестницы. На основании равенства нулю суммы моментов всех сил относительно оси, проходящей через точку В, составим уравнение:
N1lsinα − mg(cosα)l/2 = 0.
Отсюда
tgα = mg/(2N1). (3)
Выразив из уравнения (2)
N2 = mg
и подставив это значение в уравнение (1), найдем
N1 = μmg.
Подставив это выражение в формулу (3), получим:
a = arctg(1/(2μ), α = 51°.
24. Четыре шара массами m1, m2, m3 и m4 надеты на стержень так, что их центры находятся на одинаковых расстояниях l друг от друга. Масса стержня m. Определить положение центра тяжести системы.
Решение.
Предположим, что центр тяжести находится на расстоянии х от центра левого шара (рис.).
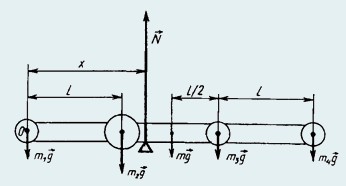
Если поставим в этом месте опору, то система будет находиться в равновесии. Следовательно, сумма моментов всех сил относительно оси, проходящей через любую точку, будет равна нулю. На систему действуют силы тяжести шаров m1g, m2g, m3g, m4g, стержня mg и сила нормальной реакции опоры N. Сумма моментов этих сил относительно оси, проходящей через точку О, равна нулю:
m2gl + mg•1,5l + m3g•2l + m4g•3l − Nx = 0.
Сумма проекций всех сил на вертикальное направление также равна нулю:
N − m1g − mg − m2g − m3g − m4g = 0.
Решив систему двух уравнений, найдем
x = (m2 + 1,5m + 2m3 + 3m4)l/(m + m1 + m2 + m3 + m4).
25. Определить положение центра тяжести однородной круглой пластины радиуса R, в которой вырезано квадратное отверстие со стороной а = R/2 так, как показано на рисунке.
Решение.
Расположим пластину с отверстием так, чтобы ось симметрии была горизонтальна, и предположим, что вырезанный квадрат помещен на прежнее место.
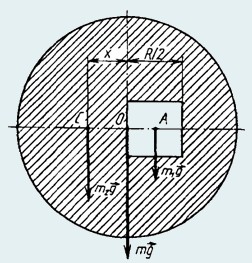
Тогда сила тяжести всего тела
mg = m1g + m2g,
где m1g − сила тяжести квадрата, приложенная в центре квадрата; m2g − сила тяжести пластинки с отверстием, приложенная в искомом центре тяжести С.
Относительно оси, проходящей через общий центр тяжести О, сумма моментов всех сил тяжести равна нулю:
m1gR/4 − m2gx = 0,
где х − расстояние от точки О до точки С (центра тяжести пластинки с отверстием). Отсюда
х = m1R/(4m2).
Пусть h − толщина пластинки, ρ − плотность материала, из которого она изготовлена. Тогда:
m1 = ρ(R/2)2h = ρR2h/4,
m2 = m − m1 = ρπR2h − ρR2h/4 = (1/4)ρR2h(4π − 1).
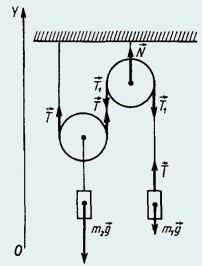
26. Система, состоящая из неподвижного и подвижного блоков, находится в равновесии. К неподвижному блоку подвешен груз массой m1 = 20 кг. Найти
массу груза m2, силу натяжения нити и силу, действующую на ось неподвижного блока.
 Решение.
Решение.
При равновесии системы сумма проекций на ось OY сил, действующих на блоки и тела, равна нулю:
2T − m2g = 0,
N − 2T1 = 0,
T − m1g = 0, (1)
где T = Т1 − модуль силы натяжения нити; N − сила реакции оси неподвижного блока.
Согласно третьему закону Ньютона, на ось этого блока действует сила F = N. Тогда из уравнений (1) найдем:
T = m1g, m2 = 2m1, F = 2T,
T = 2•102 H, m2 = 40 кг, F = 4•102 H.
27. Две пружины, жесткости которых k1 = 400 Н/м и k2 = 600 Н/м, соединены последовательно (рис.). Какой должна быть жесткость пружины, которой можно было бы заменить эту систему из двух пружин?
Решение.
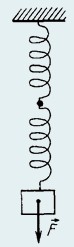 При последовательном соединении пружин силы натяжения их одинаковы и равны по модулю приложенной силе F. По закону Гука
При последовательном соединении пружин силы натяжения их одинаковы и равны по модулю приложенной силе F. По закону Гука
F = kΔl, (1)
где k − жесткость системы (а значит, и жесткость пружины, которой можно было бы заменить эту систему); Δl − абсолютная деформация системы:
Δl = Δl1 + Δl2, (2)
Δl1, Δl2 − деформация каждой пружины.
По закону Гука
F = k1Δl1, F = k2Δl2. (3)
Из выражений (1) − (3) находим:
Δl = F/k, Δl1 = F/k1, Δl2 = F/k2.
Подставив эти значения в равенство (2), получим
1/k = 1/k1 + 1/k2,
откуда
k = k1k2/(k1 + k2), k = 240 Н/м.
31. Лестница длиной 4 м приставлена к идеально гладкой стене под углом 60° к горизонту. Коэффициент трения между лестницей и полом равен 0,4. На какую максимальную высоту над полом может подняться по лестнице человек, прежде чем она начнет скользить? Масса лестницы 5 кг, человека 60 кг.
Решение.
Когда человек поднимется на максимальную высоту, то должно выполняться равенство моментов сил тяжести человека, лестницы и реакции гладкой стенки относительно точки вращения B.
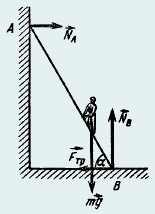
mgh/tgα + Mg(L/2)cosα = NALsinα, (1)
Так как лестница неподвижна, то выполняется равенство сил
NA = Fmp, Fmp = μNB, NB = mg + Mg.
Тогда
NA = μ(mg + Mg). (2)
Подставим (2) в (1)
mgh/tgα + Mg(L/2)cosα = μ(mg + Mg)Lsinα.
После преобразования
h = μ(m + M)Lsinαtgα/m − MLsinα/(2m).
Подставим численные значения
h = (0,4•(60 + 5)•4•sin60•tg60)/60 − 5•4•sin60°/(2•60) = 2,5 (м)
1(Ш). На стержень действуют две параллельные силы, равные F1 = 10 H и F2 = 25 Н и направленные в противоположные стороны. Определите точку приложения и величину силы, уравновешивающей силы F1 и F2, если их точки приложения находятся на расстоянии l = 1,5 м друг от друга.
Решение:
Очевидно, что модуль уравновешивающей силы F равен разности модулей действующих на стержень сил:
F = F2? F1 = 15 H.
Ясно также, что точка приложения уравновешивающей силы лежит на прямой, соединяющей точки приложения сил F1 и F, справа от большей силы. Обозначим искомое расстояние через x. Тогда по правилу моментов имеем:
F1(l + x)? F2x = 0 и x = F1l/(F2? F1) = 1 м.
Заметим, что в случае F1 = F2, т. е. когда на тело действует так называемая пара сил, уравновешивающей силы, в обычном смысле этого слава, нет. Под действием пары сил тело приходит во вращательное движение вокруг его центра тяжести.
Ответ: F = 15 H, x = 1 м.
2(Ш). К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка висит, касаясь стенки, как показано на рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой μ = 0,1. При каком угле α между нитью и стенкой катушка висит неподвижно?
Решение:
Силы, действующие на катушку, изображены на рисунке.
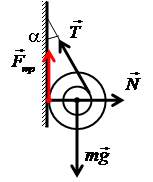
Запишем условия равновесия катушки в виде:
N – Tsinα = 0
и
Tr? FmpR = 0.
Учитывая, что Fmp = μN, получаем
sinα = r/(μR) = 1/2, и α = 30°.
Ответ: α = 30°.
4(Ш). Однородная тонкая пластинка имеет форму круга радиусом R, в котором вырезано круглое отверстие вдвое меньшего радиуса, касающегося края пластинки. Где находится ее центр тяжести?
Решение:
Из соображения симметрии ясно, что центр тяжести пластинки лежит на ее оси на некотором расстоянии x от центра круга. Если вложить обратно вырезанную часть пластинки, то центр тяжести пластинки сместится в ее центр. Запишем соответствующее правило моментов:
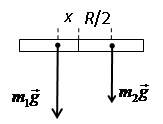
m1gx? m2gR/2 = 0,
но
m1/m2 = S1/S2 = (R2? R2/4)/(R2/4) = 3,
поэтому получаем
3x = R/2, и x = R/6.
Ответ: x = R/6.
5(Ш). На столе лежит однородный стержень массой 6 кг так, что две трети его длины находятся за краем стола. Какую силу необходимо приложить к концу стержня для удержания его в горизонтальном положении?
Решение:
На стержень действуют три силы: сила тяжести mg, удерживающая сила F и сила реакции опоры N, которая приложена в точке O, так как вначале вращения эта точка является опорой стержня.
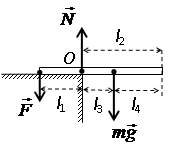
Применим правило моментов относительно оси вращения в точке O:
ΣM = 0,
Mmg + MF = 0,
mgl3? Fl1 = 0, (1)
где Mmg и MF – момент силы тяжести и приложенной силы F, а l3 и l1 – соответствующие плечи сил.
Момент силы N равен нулю, так как эта сила проходит через точку O, относительно которой рассматривается вращение, следовательно, плечо силы N равно нулю.
Из (1) находим, что
F = mgl3/l1.
Поскольку
l3 = l2? l4,
где l4 = l/2, получаем
l3 = 2l/3 – l/2 = l/6, F = mg/2.
Проводим расчет F = 6•10/2 = 30 H.
Ответ: F = 6•10/2 = 30 H.
(Ш). Куб опирается одним ребром на пол, другим – на гладкую вертикальную стенку. Определить, при каких значениях угла α возможно равновесие куба. Коэффициент трения куба о пол равен μ, ребро куба равно a.
Решение:
Уравнение проекций на вертикаль
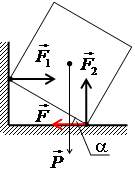
–P + F2 = 0.
Уравнение проекций на горизонталь
F1 – F = 0
F1 – реакция стенки.
Уравнение моментов относительно точки O
F1asinα = Pa(√/2)•cos(π/4 + α);
Кроме того,
F ≤ μF2.
Отсюда находим
1 > tgα ≥ 1/(2μ + 1).
Если μ > 0, то α всегда меньше π/4, так как при α > π/4 куб опрокинется.
Ответ: 1 > tgα ≥ 1/(2μ + 1); если μ > 0, то α всегда меньше π/4, так как при α > π/4 куб опрокинется.
 2015-10-14
2015-10-14 9354
9354







