| Настройки | Значение |
| Тип | Тест с оценкой |
| Всего вопросов | |
| Всего баллов | |
| Проходной балл | 3баллов |
| Показать вопросы | Все |
| Перемешивать вопросы | Да |
| Показать экран с результатами Если тест пройден | Да |
| Показать экран с результатами Если тест провален | Да |
| Ограничение по времени | 0:20:0 |
| 1. Укажите правильную формулу теоремы косинусов: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 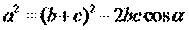
| |
| (+) | 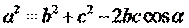
| |
| () | 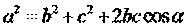
| |
| () | 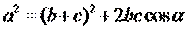
|
| 2. Укажите общее уравнение плоскости: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 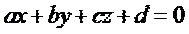
| |
| () | 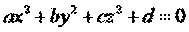
| |
| () | 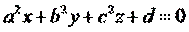
| |
| () | 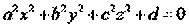
|
| 3. Если объем пирамиды АВСМ равен V, то расстояние от точки M до плоскости α, содержащей треугольник АВС, вычисляют по формуле: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 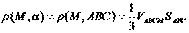
| |
| () | 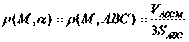
| |
| () | 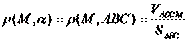
| |
| (+) | 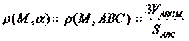
|
| 4. Угол между параллельными прямыми равен: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 0º | |
| () | 180º | |
| () | 360º | |
| () | данный угол не измеряется |
| 5. Теорема о трех косинусах записывается в виде формулы (где α, β, γ – плоские углы, А – двугранный угол, составленный плоскостями углов β и γ): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 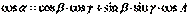
| |
| () | 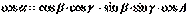
| |
| () | 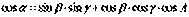
| |
| () | 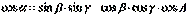
|
| 6. Если α, β и γ – углы, которые образует некоторая прямая с тремя попарно перпендикулярными прямыми, то справедливо следующее равенство: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 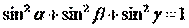
| |
| () | 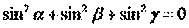
| |
| (+) | 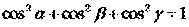
| |
| () | 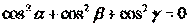
|
| 7. Угол между прямой l и плоскостью α можно вычислить по формуле (см. условие для формул на рисунке): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | 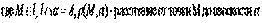
| |
| () | 
| |
| (+) | 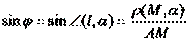
| |
| () | 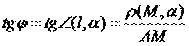
| |
| () | 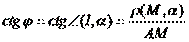
| |
| 8. Укажите формулу боковой поверхности правильной пирамиды (где l – длина бокового ребра, Р – периметр основания): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 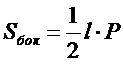
| |
| () | 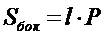
| |
| (+) | 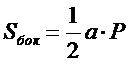
| |
| () | 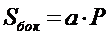
|
| 9. Полная поверхность правильного тетраэдра равна (где а – сторона, Р – периметр основания): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 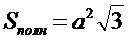
| |
| () | 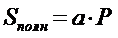
| |
| () | 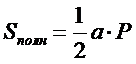
| |
| () | 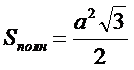
|
| 10. Если пересечь пирамиду плоскостью, параллельной основанию, то: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | площади сечения и основания будут относится друг к другу как квадраты начального бокового ребра и отрезка бокового ребра от вершины пирамиды до сечения | |
| (+) | площади сечения и основания будут относится друг к другу как квадраты их расстояний от вершины пирамиды | |
| () | площади сечения и основания будут относится друг к другу как длина начального бокового ребра к отрезку бокового ребра от вершины пирамиды до сечения | |
| () | площади сечения и основания будут относится друг к другу как их расстояния от вершины пирамиды |
| 11. Формула объема прямой призмы имеет вид (где l – длина бокового ребра, h – высота призмы, Sосн – площадь основания): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 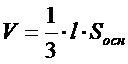
| |
| () | 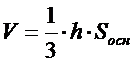
| |
| () | 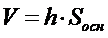
| |
| (+) | 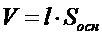
|
| 12. Объем произвольной пирамиды равен (где h – высота пирамиды, Sосн – площадь основания): (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 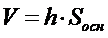
| |
| () | 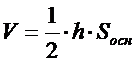
| |
| (+) | 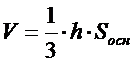
| |
| () | 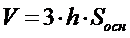
|
 2015-10-13
2015-10-13 311
311







