Особенности вычислений в простых полях Галуа

Введение

Вычисления над кольцами и в простых полях

Алгебраические системы - это системы, которые подчиняются определённым правилам или законам. В большей части это те же законы, которые приложимы к обычным числовым системам. Так группа - система в которой заданы одна основная операция и операция ей обратная, например сложение и вычитание или умножение и деление. В кольце определены две основные операции. Сложение и умножение и операция обратная первой (вычитание). В поле определены две основные операции и две обратные операции.

Алгебраическая группа

Группой называется совокупность объектов или элементов, для которых определена некоторая операция и выполняются аксиомы G1-G4. Операцию обычно называют сложением или умножением, даже если она не является арифметическим сложением или умножением

G1 (замкнутость) Операция может быть применена к любым двум элементам группы, в результате получается третий элемент группы.

G2 (ассоциативный закон) Для любых трёх элементов a, b, c группы (a+b)+c = a+(b+c) для сложения или (ab)c=a(bc) для умножения.

G3 Существует единичный элемент. Для сложения a+0=a или для умножения a´1=a

G4 Каждый элемент группы имеет обратный

Если кроме аксиом G1-G4 выполняются условие коммутативности или a+b=b+a то группу называют коммутативной или абелевой.

Алгебраическое кольцо

Кольцом R называется множество элементов над которым определены две операции. Одна называется сложением, а вторая умножением, даже если эти операции не являются обычным арифметическим сложением и умножением чисел. Для того чтобы множество R было кольцом должны выполняться следующие аксиомы:

R1 Множество R является абелевой группой относительно операции сложения

R2 (замкнутость) Для любых двух элементов a и b из множества R определено произведение ab, которое является элементом R

R3 (ассоциативный закон) Для любых трёх элементов a, b, с из множества R выполняется a(bc)=(ab)c

R4 (дистрибутивный закон) Для любых трёх элементов a, b, с из множества R выполняется a(b+c)=ab+ac и (b+c)a=ba+ca.

Кольцо называется коммутативным, если коммутативна операция умножения, т. е. если для любых двух элементов a и b из множества R ab=ba

Поле Галуа

Полем называется коммутативное кольцо с единичным элементом относительно умножения в котором каждый не нулевой элемент имеет обратный элемент по умножению.

Поля в которых определена операция сложения и умножения по модулю простого числа называются простыми полями. Для другого количества элементов поля существуют не всегда.

Особенности вычислений в простых полях Галуа

Сложение

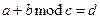
В результате вычислений искомый результат находится в пределах 0£ d < c.

Если (a+b)³c, то d приравнивается к остатку от целочисленного деления суммы (a+b) на c

Например:

1+1 mod 2 = 0;

3+5 mod 7 = 1;

4+4 mod 5 = 3.

Вычитание

В результате вычислений искомый результат находится в пределах 0£ d < c.

Если (a-b)<0, то к разности прибавляется c приравнивается к остатку от целочисленного деления суммы (a+b) на c

Например:

2–1 mod 3 = 1;

3–5 mod 7 = 5;

4–4 mod 5 = 0.

Умножение

В результате вычислений искомый результат находится в пределах 0£ d < c.

Если (a´b)³c, то d приравнивается к остатку от целочисленного деления произведения (a´b) на c

Например:

1´1 mod 2 = 1;

3´5 mod 7 = 1;

4´4 mod 8 = 0.

Деление

Операция деления определена как операция обратная умножению и существует только в полях Галуа

В результате вычислений искомый результат находится в пределах 0£ d < c.

Конструктивного алгоритма вычисления частного в простом поле не существует, поэтому деление выполняется методом перебора так:

В качестве первого множителя фиксируется число a;

Цикл по d = от 0 до (C-1)

Выполняется умножение в поле ;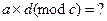

Если произведение равно b то результат найден

Конец цикла.

Возведение в степень

В результате вычислений искомый результат находится в пределах 0£ d < c.

Если (a^b)³c, то d приравнивается к остатку от целочисленного деления результата (a^b) на c

Например:

2⁴ mod 7 = 2;

4³ mod 11 = 9;

5⁴ mod 9 = 4.

При возведении в степень область значений степенной функции в поле Галуа или над кольцом может быть меньше, чем область значений аргументов степенной функции

Извлечение дискретного логарифма

Операция дискретного логарифмирования определена как операция обратная возведению в степень. Найти обозначает найти такое число d, что при возведении a в эту степень получим число b.

В результате вычислений искомый результат находится в пределах 0£ d < c.

Конструктивного алгоритма вычисления логарифма в простом поле не существует, поэтому логарифмирование выполняется методом перебора так:

В качестве основания логарифма фиксируется число a;

Цикл по d = от 0 до (C-1)

Выполняется возведение в степень[1] ;

Если показательная функция равна b то результат найден

Конец цикла.

Следует отметить, что дискретный логарифм существует не всегда. Так например:

log₄9 mod 11 = 3;

log₄8 mod 11 – не существует потому что 4 в любой степени (от 0 до 10 по модулю 11) никогда не равно 8.